题目内容
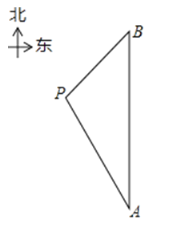
【题目】在一次海上救援中，两艘专业救助船
同时收到某事故渔船的求救讯息，已知此时救助船
在
的正北方向，事故渔船
在救助船的北偏西30°方向上，在救助船的西南方向上，且事故渔船与救助船相距120海里．
（1）求收到求救讯息时事故渔船与救助船之间的距离；
（2）若救助船A，分别以40海里/小时、30海里/小时的速度同时出发，匀速直线前往事故渔船处搜救，试通过计算判断哪艘船先到达．
【答案】（1）收到求救讯息时事故渔船
与救助船
之间的距离为
海里；（2）救助船先到达．
【解析】
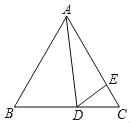
(1)如图，作
于
，在△PAC中先求出PC的长，继而在△PBC中求出BP的长即可；
(2)根据“时间=路程÷速度”分别求出救助船A和救助船B所需的时间，进行比较即可.
(1)如图，作于，
则
，
由题意得：
海里，
，
，
∴
海里，
是等腰直角三角形，
∴
海里，
海里，
答：收到求救讯息时事故渔船与救助船之间的距离为海里；
(2)∵
海里，
海里，救助船
分别以40海里/小时、30海里/小时的速度同时出发，
∴救助船
所用的时间为
(小时)，
救助船所用的时间为
(小时)，
∵
，
∴救助船先到达．
练习册系列答案
相关题目
