题目内容
【题目】如图所示，某大学的楼门是一抛物线形水泥建筑物，大门的地面宽度为
，两侧距离地面
高处各有一个挂校名横匾用的铁环，两铁环的水平距离为
，则校门的高约为(精确到
，水泥建筑物的厚度忽略不计)( )
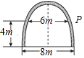
A. 9.2m B. 9.1m C. 9.0m D. 8.9m
【答案】B
【解析】
由题意可知，以地面为x轴，大门左边与地面的交点为原点建立平面直角坐标系，抛物线过（0，0）、（8，0）、（1、4）、（7、4），运用待定系数法求出解析式后，求函数值的最大值即可．
解：以地面为x轴，大门左边与地面的交点为原点建立平面直角坐标系，
则抛物线过O（0，0）、E（8，0）、A（1、4）、B（7、4）四点，
设该抛物线解析式为：y＝ax2＋bx＋c，
则
，
解得：
.
．
故函数解析式为：y＝－
x2＋
x．
当x＝4时，可得y＝－
≈9.1米，
故选：B．
练习册系列答案
黄冈创优卷系列答案
相关题目
