题目内容
[(1)-(3),10分]如图,已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC(或其延长线)的距离分别为h1、h2、h3,△ABC的高为h.在图(1)中,点P是边BC的中点,此时h3=0,可得结论:h1+h2+h3=h.
在图(2)--(5)中,点P分别在线段MC上、MC延长线上、△ABC内、△ABC外.
(1)请探究:图(2)--(5)中,h1、h2、h3、h之间的关系;(直接写出结论)
(2)证明图(2)所得结论;
(3)证明图(4)所得结论.
(4)在图(6)中,若四边形RBCS是等腰梯形,∠B=∠C=60°,RS=n,BC=m,点P在梯形内,且点P到四边BR、RS、SC、CB的距离分别是h1、h2、h3、h4,桥形的高为h,则h1、h2、h3、h4、h之间的关系为:______;图(4)与图(6)中的等式有何关系?

【答案】分析:(1)图②-⑤中的关系依次是h1+h2+h3=h; h1-h2+h3=h; h1+h2+h3=h;h1+h2-h3=h.
(2)解直角三角形得出h1=BPsin60°,h2=PCsin60°,h3=0,求出h1+h2+h3=ACsin60°,即可得出答案;
(3)根据三角形面积公式和等边三角形性质得出 BC×AM=
BC×AM= AB×PD+
AB×PD+ AC×PE+
AC×PE+ BC×PF,AB=BC=AC,即可得出答案;
BC×PF,AB=BC=AC,即可得出答案;
(4)连接CP,BP,RP,过R作RQ⊥BC于Q,求出BR、CS,根据面积公式求出即可.
解答:解:(1)图②-⑤中的关系依次是:
h1+h2+h3=h; h1-h2+h3=h; h1+h2+h3=h;h1+h2-h3=h.
(2)图②中,h1+h2+h3=h.
证明:∵h1=BPsin60°,h2=PCsin60°,h3=0,
∴h1+h2+h3=BPsin60°+PCsin60°
=BCsin60°
=ACsin60°
=h.
(3)证明:如图,

连接AP、BP、CP,
S△ABC=S△PAC+S△PBC+S△PAB,
∴ BC×AM=
BC×AM= AB×PD+
AB×PD+ AC×PE+
AC×PE+ BC×PF,
BC×PF,
∵AB=BC=AC,
∴PD+PE+PF=AM,
即h1+h2+h3=h;
(4)
连接CP,BP,RP,过R作RQ⊥BC于Q,
则RQ∥SF,
∵RS∥BC,
∴四边形RQFS是平行四边形,
∴RS=QF=n,
∵梯形RBCS是等腰梯形,
∴BQ=FC= (m-n),
(m-n),
∵∠B=∠C=60°,
∴BR=CS=2BQ=(m-n),
∴S梯形BCRS=S△BRP+S△BCP+S△CSP+S△RPS,
∴ •(m-n)•h1+
•(m-n)•h1+ •m•h2+
•m•h2+ •(m-n)•h3+
•(m-n)•h3+ •n•h4=
•n•h4= (m+n)h
(m+n)h
∴(m-n)h1+mh2+(m-n)h3+nh4=(m+n)h,
m(h1+h2+h3)-n(h1+h3-h4)=(m+n)h,
∴图(4)与图(6)中的等式有当n=0时,图形(6)的等式就变成图形(4)的等式,
故答案为:m(h1+h2+h3)-n(h1+h3-h4)=(m+n)h.
点评:本题考查了三角形面积,平行四边形性质和判定,等腰梯形性质,解直角三角形的应用,主要考查学生综合运用性质进行计算的能力,题目比较好,由一定的难度.
(2)解直角三角形得出h1=BPsin60°,h2=PCsin60°,h3=0,求出h1+h2+h3=ACsin60°,即可得出答案;
(3)根据三角形面积公式和等边三角形性质得出
 BC×AM=
BC×AM= AB×PD+
AB×PD+ AC×PE+
AC×PE+ BC×PF,AB=BC=AC,即可得出答案;
BC×PF,AB=BC=AC,即可得出答案;(4)连接CP,BP,RP,过R作RQ⊥BC于Q,求出BR、CS,根据面积公式求出即可.
解答:解:(1)图②-⑤中的关系依次是:
h1+h2+h3=h; h1-h2+h3=h; h1+h2+h3=h;h1+h2-h3=h.
(2)图②中,h1+h2+h3=h.
证明:∵h1=BPsin60°,h2=PCsin60°,h3=0,
∴h1+h2+h3=BPsin60°+PCsin60°
=BCsin60°
=ACsin60°
=h.
(3)证明:如图,

连接AP、BP、CP,
S△ABC=S△PAC+S△PBC+S△PAB,
∴
 BC×AM=
BC×AM= AB×PD+
AB×PD+ AC×PE+
AC×PE+ BC×PF,
BC×PF,∵AB=BC=AC,
∴PD+PE+PF=AM,
即h1+h2+h3=h;
(4)

连接CP,BP,RP,过R作RQ⊥BC于Q,
则RQ∥SF,
∵RS∥BC,
∴四边形RQFS是平行四边形,
∴RS=QF=n,
∵梯形RBCS是等腰梯形,
∴BQ=FC=
 (m-n),
(m-n),∵∠B=∠C=60°,
∴BR=CS=2BQ=(m-n),
∴S梯形BCRS=S△BRP+S△BCP+S△CSP+S△RPS,
∴
 •(m-n)•h1+
•(m-n)•h1+ •m•h2+
•m•h2+ •(m-n)•h3+
•(m-n)•h3+ •n•h4=
•n•h4= (m+n)h
(m+n)h∴(m-n)h1+mh2+(m-n)h3+nh4=(m+n)h,
m(h1+h2+h3)-n(h1+h3-h4)=(m+n)h,
∴图(4)与图(6)中的等式有当n=0时,图形(6)的等式就变成图形(4)的等式,
故答案为:m(h1+h2+h3)-n(h1+h3-h4)=(m+n)h.
点评:本题考查了三角形面积,平行四边形性质和判定,等腰梯形性质,解直角三角形的应用,主要考查学生综合运用性质进行计算的能力,题目比较好,由一定的难度.

练习册系列答案
相关题目
初三(1)班某一次数学测验成绩如下:
63,84,91,53,69,81,61,69,91,78,75,81,80,67,76,81,79,94,61,69,89,70,70,87,81,86,90,88,85,67,71,82,87,75,87,95,53,65,74,77.
数学老师按10分的组距分段,统计每个分数段出现的频数,填入频数分布表,并绘制频数分布直方图.
(1)请把频数分布表及频数分布直方图补充完整;
(2)请说明哪个分数段的学生最多?哪个分数段的学生最少?
(3)请你帮老师统计一下这次数学考试的及格率(60分以上含60分为及格)及优秀率(90分以上含90分为优秀).
63,84,91,53,69,81,61,69,91,78,75,81,80,67,76,81,79,94,61,69,89,70,70,87,81,86,90,88,85,67,71,82,87,75,87,95,53,65,74,77.

数学老师按10分的组距分段,统计每个分数段出现的频数,填入频数分布表,并绘制频数分布直方图.
| 成 绩 段 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~99.5 |
| 频数纪录 | 丅 | 正  |
正正 |
正正  |
正 |
| 频 数 | 2 | 9 | 14 | 5 | |
| 频 率 | 0.050 | 0.225 | 0.250 | 0.350 |
(2)请说明哪个分数段的学生最多?哪个分数段的学生最少?
(3)请你帮老师统计一下这次数学考试的及格率(60分以上含60分为及格)及优秀率(90分以上含90分为优秀).
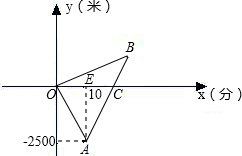 校.已知小欣步行速度为每分50米,求小欣家与学校距离及小欣早晨上学需要的时间.
校.已知小欣步行速度为每分50米,求小欣家与学校距离及小欣早晨上学需要的时间.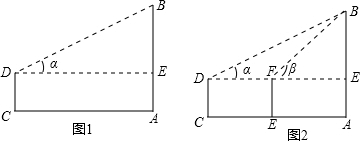 ,向塔的方向前进20米到E处,又测得塔顶端B的仰角β=45°.求塔AB的高(精确到0.1米).
,向塔的方向前进20米到E处,又测得塔顶端B的仰角β=45°.求塔AB的高(精确到0.1米).