题目内容
如图，D、E分别是AB、AC上两点，CD与BE相交于点O，现给出下列4个条件：（1）∠ADC=∠AEB；（2）
| AD |
| AC |
| AE |
| AB |
| AD |
| AB |
| AE |
| AC |
| OD |
| OB |
| OE |
| OC |
在上述4个条件中选取一个，能使△BOD∽△COE的选法有（ ）
分析：根据已知及相似三角形的判定方法进行分析，从而得到答案．
解答：解：∵∠DOB=∠EOC，
∴当∠B=∠C或∠ADC=∠AEB或
=
时△BOD∽△COE，
故选C．
∴当∠B=∠C或∠ADC=∠AEB或
| OD |
| OB |
| OE |
| OC |
故选C．
点评：此题考查了相似三角形的判定，①有两个对应角相等的三角形相似；②有两个对应边的比相等，且其夹角相等，则两个三角形相似；③三组对应边的比相等，则两个三角形相似．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
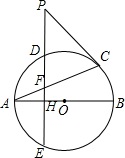如图：AB、AC分别是⊙O的直径和弦，D为弧AC上一点，DE⊥AB于点H，交⊙O于点E，交AC于点F．P为ED延长线上一点，连PC．
如图，AB和AC分别是⊙O的直径和弦，OD⊥AC于D点，若OA=4，∠A=30°，则BD等于（ ）
已知：如图，E、F分别是正方形ABCD边BC、AD上的点，且BE=DF
桌上放着一个圆柱和一个长方体，如图（1），请说出下列三幅图（如图（2））分别是从哪个方向看到的．