题目内容
已知正方形内接于圆心角为90°,半径为10的扇形(即正方形的各顶点都在扇形上),则这个正方形的边长为________.
5 或2
或2
分析:根据题意画出图形,由于正方形内接于扇形,故应分两种情况进行讨论.
解答: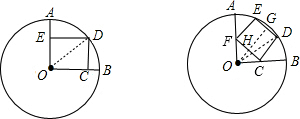 解:如图1所示:
解:如图1所示:
连接OD,设正方形OCDE的边长为x,
则在Rt△OCD中,
OD2=OC2+CD2,即102=x2+x2,
解得x=5 ;
;
如图2所示,
过O作OG⊥DE,交CF于点H,连接OD,
设FH=a,
∵四边形CDEF是正方形,
∴OH⊥CF,△OCF是等腰直角三角形,
∴FH=CH=a,
∵∠AOC=90°,
∴CH=OH,
∴OG=3a,
在Rt△ODG中,
OD2=GD2+OG2,即102=a2+(3a)2,
解得a= ,
,
∴CF=2a=2 .
.
故答案为:5 或2
或2 .
.
点评:本题考查的是垂径定理及勾股定理,解答此题的关键是根据题意画出图形,作出辅助线,构造出直角三角形,再进行解答.
 或2
或2
分析:根据题意画出图形,由于正方形内接于扇形,故应分两种情况进行讨论.
解答:
 解:如图1所示:
解:如图1所示:连接OD,设正方形OCDE的边长为x,
则在Rt△OCD中,
OD2=OC2+CD2,即102=x2+x2,
解得x=5
 ;
;如图2所示,
过O作OG⊥DE,交CF于点H,连接OD,
设FH=a,
∵四边形CDEF是正方形,
∴OH⊥CF,△OCF是等腰直角三角形,
∴FH=CH=a,
∵∠AOC=90°,
∴CH=OH,
∴OG=3a,
在Rt△ODG中,
OD2=GD2+OG2,即102=a2+(3a)2,
解得a=
 ,
,∴CF=2a=2
 .
.故答案为:5
 或2
或2 .
.点评:本题考查的是垂径定理及勾股定理,解答此题的关键是根据题意画出图形,作出辅助线,构造出直角三角形,再进行解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

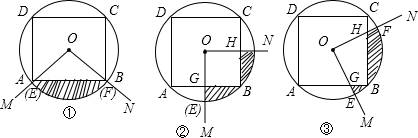
 及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
 及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
 及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
 及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①
及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①