题目内容
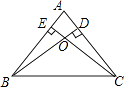
【题目】如图，正方形ABCD的边长为1，点P在射线BC上（异于点B、C），直线AP与对角线BD及射线DC分别交于点F、Q 
（1）若BP= 
，求∠BAP的度数；
（2）若点P在线段BC上，过点F作FG⊥CD，垂足为G，当△FGC≌△QCP时，求PC的长；
（3）以PQ为直径作⊙M． ①判断FC和⊙M的位置关系，并说明理由；
②当直线BD与⊙M相切时，直接写出PC的长．
【答案】
（1）解：∵四边形ABCD是正方形，
∴∠ABP=90°，
∴tan∠BAP= 
= 
= 
，
∵tan30°= ，
∴∠BAP=30°
（2）解：如图1，设PC=x，则BP=1﹣x，
∵△FGC≌△QCP，
∴GC=PC=x，DG=1﹣x，
∵∠BDC=45°，∠FGD=90°，
∴△FGD是等腰直角三角形，
∴FG=DG=CQ=1﹣x，
∵AB∥DQ，
∴ 
，
∴ 
，
∴x=（1﹣x）2，
解得：x1= 
＞1（舍去），x2= 
，
∴PC=
（3）解：①如图2，当点P在线段BC上时，FC与⊙M相切，理由是：
取PQ的中点M，以M为圆心，以PQ为直径画圆，连接CM，
∵∠PCQ=90°，PQ为直径，
∴点C是圆M上，
∵△PCQ为直角三角形，
∴MC=PM，
∴∠MCP=∠MPC，
∵∠APB=∠MPC，
∴∠MCP=∠APB，
∵∠APB+∠BAP=90°，
∴∠MCP+∠BAP=90°，
∵AD=DC，∠ADB=∠CDB，FD=FD，
∴△ADF≌△CDF，
∴∠FAD=∠FCD，
∵∠BAP+∠FAD=∠BCF+∠FCD，
∴∠BAP=∠BCF，
∴∠MCP+∠BCF=90°，
∴FC⊥CM，
∴FC与⊙M相切；
如图3，当点P在线段BC的延长线上时，FC与⊙M也相切，理由是：
取PQ的中点M，以M为圆心，以PQ为直径画圆，连接CM，
同理得∠AQD=∠MCQ，点C是圆M上，
∵AD=DC，∠BDA=∠CDB=45°，DF=DF，
∴△ADF≌△CDF，
∴∠FAD=∠FCD，
∵∠AQD+∠FAD=90°，
∴∠MCD+∠FCD=90°，
∴FC⊥MC，
∴FC与⊙M相切；
：②当点P在线段BC上时，如图4，
设⊙M切BD于E，连接EM、MC，
∴∠MEF=∠MCF=90°，
∵ME=MC，MF=MF，
∴△MEF≌△MCF，
∴∠QFC=∠QFE，
∵∠BAP=∠Q=∠BCF，
设∠Q=x，则∠BAP=∠BCF=x，∠QFE=∠QFC=45°+x，∠DFC=45°+x，
∵∠QFE+∠QFC+∠DFC=180°，
∴3（45+x）=180，
x=15，
∴∠Q=15°，
∴∠BAP=15°，
作AP的中垂线HN，交AB于H，交AP于N，
∴AH=AP，
∴∠BHP=30°，
设BP=x，则HP=2x，HB= 
x，
∴2x+ x=1，
x=2﹣ ，
∴PC=BC﹣BP=1﹣（2﹣ ）= ﹣1；
当点P在点C的右侧时（即在线段BC的延长线上），如图5，
同理可得：PC= +1；
综上所述：PC= ﹣1或 +1．
【解析】（1）在直角△ABP中，利用特殊角的三角函数值求∠BAP的度数；（2）设PC=x，根据全等和正方形性质得：QC=1﹣x，BP=1﹣x，由AB∥DQ得 ，代入列方程求出x的值，因为点P在线段BC上，所以x＜1，写出符合条件的PC的长；（3）①如图2，当点P在线段BC上时，FC与⊙M相切，只要证明FC⊥CM即可，先根据直角三角形斜边上的中线得CM=PM，则∠MCP=∠MPC，从而可以得出∠MCP+∠BAP=90°，再证明△ADF≌△CDF， 得∠FAD=∠FCD，则∠BAP=∠BCF，所以得出∠MCP+∠BCF=90°，FC⊥CM；
如图3，当点P在线段BC的延长线上时，FC与⊙M相切，同理可得∠MCD+∠FCD=90°，则FC⊥CM，FC与⊙M相切；②当点P在线段AB上时，如图4，设⊙M切BD于E，连接EM、MC，设∠Q=x，根据平角BFD列方程求出x的值，作AP的中垂线HN，得∠BHP=30°，在Rt△BHP中求出BP的长，则得出PC= ﹣1；当点P在点C的右侧时（即在线段BC的延长线上），如图5，同理可得：PC= +1．
