题目内容
【题目】某公司有A型产品40件，B型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完.两商店销售这两种产品每件的利润（元）如下表.设分配给甲店A型产品
件，这家公司卖出这100件产品的总利润为W（元）.
（1）求W关于的函数关系式，并求出的取值范围；
（2）若公司要求总利润不低于17560元，说明有多少种不同分配方案？
（3）实际销售过程中，公司发现这批产品尤其是A型产品很畅销，便决定对甲店的最后21件A型产品每件提价
元销售（为正整数）.两店全部销售完毕后结果的总利润为18000元，求 值.并写出公司这100件产品对甲乙两店是如何分配的？
【答案】（1）
，
的整数；（2）有3种不同分配方案；（3）甲店：A型 39件 B型 31件；乙店：A型 1件 B型 29件.
【解析】
（1）设分配给甲店A型产品x件，则分配给甲店B型产品（70-x）件，分配给乙店A型产品（40-x）件，分配给乙店B型产品（x-10）件，然后根据它们的利润得到W=200x+170（70-x）+160（40-x）+150[30-（40-x）]，然后整理即可；然后利用x≥0，40-x≥0，30-（40-x）≥0可得到x的取值范围；
（2）根据W≥17560得到关于x的不等式以及（1）中x的取值范围可得到整数x为38、39、40，即有三种不同的分配方案；
（3）根据题意总利润为W加上21a等于18000，即20x+16800+21a=18000，整理得：21a+20x=1200，然后把x的值分别代入计算确定a的值，同时得到分配方案．
解：（1）
由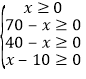
，
∴的整数.
∴，的整数.
（2）由题
∴
又
∴
的整数.∴
∴有3种不同分配方案
（3）由题
∴
当
时，
舍
当
时，
当
时，
舍
∴
公司对100件产品分配如下：甲店：A型 39件 B型 31件；乙店：A型 1件 B型 29件.
