题目内容
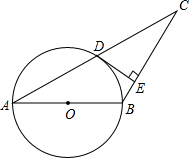
如图，已知△ABC内接于⊙O，点D在OC的延长线上，∠B=∠D=30°．
（1）AD是⊙O的切线吗？说明理由；
（2）若OD⊥AB，BC=5，求AD的长；
（3）在（2）的前提下，连接BD，则BD和⊙O及AD有何关系？简要说明理由．
（1）AD是⊙O的切线吗？说明理由；
（2）若OD⊥AB，BC=5，求AD的长；
（3）在（2）的前提下，连接BD，则BD和⊙O及AD有何关系？简要说明理由．
（1）AD是⊙O的切线．
理由：连接AD，
∵∠B=30°，
∴∠AOD=2∠B=60°，
∵∠D=30°，
∴∠OAD=90°，
即OA⊥AD，
∴AD是⊙O的切线；
（2）∵OD⊥AB，BC=5，
∴AC=BC=5，
∵OA=OC，∠AOC=60°，
∴△AOC是等边三角形，
∴OA=AC=5，
∵OA⊥AD，∠D=30°，
∴OD=2OA=10，
∴AD=
=5
；
（3）连接OB，
∵OD⊥AB，
∴BE=AE，
∴AD=BD，
在△OBD和△OAD中，
，
∴△OBD≌OAD（SSS），
∴∠OBD=∠OAD=90°，
即OB⊥BD，
∴BD是⊙O的切线．
理由：连接AD，
∵∠B=30°，
∴∠AOD=2∠B=60°，
∵∠D=30°，
∴∠OAD=90°，
即OA⊥AD，
∴AD是⊙O的切线；
（2）∵OD⊥AB，BC=5，∴AC=BC=5，
∵OA=OC，∠AOC=60°，
∴△AOC是等边三角形，
∴OA=AC=5，
∵OA⊥AD，∠D=30°，
∴OD=2OA=10，
∴AD=
| OD2-OA2 |
| 3 |
（3）连接OB，
∵OD⊥AB，
∴BE=AE，
∴AD=BD，
在△OBD和△OAD中，
|
∴△OBD≌OAD（SSS），
∴∠OBD=∠OAD=90°，
即OB⊥BD，
∴BD是⊙O的切线．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，切点为N，且AN=3．将Rt△ABC绕A顺时针旋转120°后得到Rt△ADE，点B、C的对应点分别是点D、E．
