题目内容
 如图,以点O为圆心的三个同心圆把以OA为半径的大圆O的面积四等分,求这个三个圆的半径OB,OC,OD的长.
如图,以点O为圆心的三个同心圆把以OA为半径的大圆O的面积四等分,求这个三个圆的半径OB,OC,OD的长.考点:算术平方根
专题:
分析:根据每个圆与大圆的面积关系,即可求出每个圆的半径长.
解答:解:∵π•OD2=
π•OA2,
∴OD2=
OA2,
∴OD=
OA;
∵π•OC2=
π•OA2,
∴OC2=
OA2,
∴OC=
OA;
∵π•OB2=
π•OA2,
∴OB2=
OA2,
∴OB=
OA;
因此这三个圆的半径为:OB=
OA,OC=
OA,OD=
OA.
| 1 |
| 4 |
∴OD2=
| 1 |
| 4 |
∴OD=
| 1 |
| 2 |
∵π•OC2=
| 1 |
| 2 |
∴OC2=
| 1 |
| 2 |
∴OC=
| ||
| 2 |
∵π•OB2=
| 3 |
| 4 |
∴OB2=
| 3 |
| 4 |
∴OB=
| ||
| 2 |
因此这三个圆的半径为:OB=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查了算术平方根的定义和性质;弄清每个圆与大圆的面积关系是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
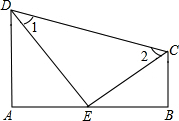 如图,已知DA⊥AB,DE平分∠ADC,CE平分∠DCB,且∠1+∠2=90°,试说明BC⊥AB.
如图,已知DA⊥AB,DE平分∠ADC,CE平分∠DCB,且∠1+∠2=90°,试说明BC⊥AB. 表示4xyz,“方框”
表示4xyz,“方框” 表示-5abdc,求
表示-5abdc,求 ×
× 的值.
的值.