题目内容
【题目】如图,已知 OACB 的顶点 O、A、B 的坐标分别是(0,a)、(b,0),且a、b 满足![]()
![]()
![]() b .
b .
(1)如图 1,a= ,b= ,点 C 的坐标 .
(2)如图 2,点 P 为边 OB 上一动点,将线段 AP 绕 P 点顺时针旋转 90°至 PD.当点 P 从O 运动到 B 的过程中,求点 D 运动路径的长度.
(3)如图 3,在(2)的条件下,作等腰 Rt△BED,且∠DBE=90°,再作等腰 Rt△ECF, 且∠ECF=90°,直线 FE 分别交 AC、OB 于点 M、N,求证:FM=EN.



【答案】(1)![]() ;
;![]() ;(
;(![]() ,
,![]() );(2)
);(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)根据![]()
![]()
![]() b 可得
b 可得![]() 且
且![]() ,从而确定a的值,代入求得b的值,然后利用平行四边形的性质确定点C的坐标;
,从而确定a的值,代入求得b的值,然后利用平行四边形的性质确定点C的坐标;
(2)点P的运动轨迹为一条线段,则点D的运动轨迹也为一条线段,当点P与点O重合时,点D与点B重合,当点P与点B重合时,点D的位置如图1所示,点D的运动路径为BD,然后利用正方形和旋转的性质算出BD=![]() ;
;
(3)由(2)点D的运动路径可知点D在∠OBC的外角平分线上,过点F作FG垂直AC于点G,过E作EH垂直AC于点H,已知△FCE为等腰直角三角形,可推出△FGC≌△CHE(AAS),过点E作EQ垂直OB于点Q,可推出△FGM≌△ENQ(AAS),可得FM=EN.
解:∵![]()
![]()
![]() b
b
∴![]() 且
且![]()
解得![]()
∴将![]() 代入
代入![]()
![]()
![]() b
b
∴b=![]()
∴A(0,![]() )、B(
)、B(![]() ,0)
,0)
∴OA=OB=![]() ,
,
∵四边形OACB为平行四边形,∠AOB=90°,
∴四边形OACB为正方形,
∴C点坐标为(![]() ,
,![]() )
)
故答案为:![]() ;
;![]() ;(
;(![]() ,
,![]() );
);
(2)如图1所示,
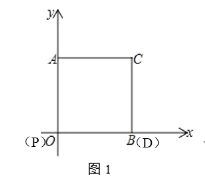
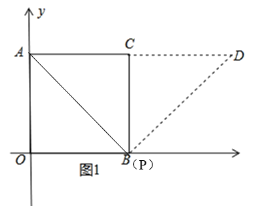
∵点P的运动轨迹为一条线段,则点D的运动轨迹也为一条线段,
当点P与点O重合时,点D与点B重合,当点P与点B重合时,点D的位置如图1所示,
∴点D的运动路径为BD,
又∵线段 AP 绕 P 点顺时针旋转 90°至 PD且由(1)可知四边形四边形OACB为正方形
∴BD=AB=![]() ;
;
(3)如图2所示,
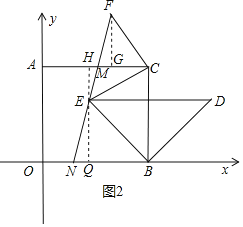
由(2)点D的运动路径可知点D在∠OBC的外角平分线上,
∴∠DBC=∠EBC=∠EBO=45°,
∴ED∥OB,
过点F作FG垂直AC于点G,过E作EH垂直AC于点H,
∴∠FGC=∠EHC=90°,
∵△FCE为等腰直角三角形,
∴FC=EC,∠FCE=90°,
∵∠ACB=90°,
∴∠FCG=∠ECB=∠CEH,
∴△FGC≌△CHE(AAS),
∴CH=FG,
过点E作EQ垂直OB于点Q,
则BQ=EQ=CH=FG,
∵∠FGM=∠EQN=90°,
∠FMG=∠ENQ,
∴△FGM≌△ENQ(AAS),
∴FM=EN.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案