ЬтФПФкШн
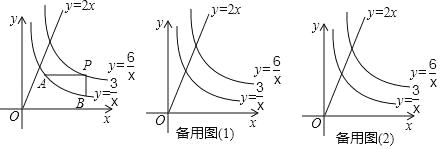
ЁОЬтФПЁПвбжЊЕуPЃЈmЃЌnЃЉЪЧЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЕФвЛЖЏЕуЃЌPAЁЮxжсЃЌPBЁЮyжсЃЌЗжБ№НЛЗДБШР§КЏЪ§yЃН
ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЕФвЛЖЏЕуЃЌPAЁЮxжсЃЌPBЁЮyжсЃЌЗжБ№НЛЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓгкЕуAЃЌBЃЌЕуCЪЧжБЯпyЃН2xЩЯЕФвЛЕуЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓгкЕуAЃЌBЃЌЕуCЪЧжБЯпyЃН2xЩЯЕФвЛЕуЃЎ
ЃЈ1ЃЉЕуAЕФзјБъЮЊЃЈЁЁ ЁЁЃЌЁЁ ЁЁЃЉЃЌЕуBЕФзјБъЮЊЃЈЁЁ ЁЁЃЌЁЁ ЁЁЃЉЃЛЃЈгУКЌmЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉдкЕуPдЫЖЏЕФЙ§ГЬжаЃЌСЌНгABЃЌжЄУїЃКЁїPABЕФУцЛ§ЪЧвЛИіЖЈжЕЃЌВЂЧѓГіетИіЖЈжЕЃЛ
ЃЈ3ЃЉдкЕуPдЫЖЏЕФЙ§ГЬжаЃЌвдЕуPЃЌAЃЌBЃЌCЮЊЖЅЕуЕФЫФБпаЮФмЗёЮЊЦНааЫФБпаЮЃПШєФмЃЌЧѓГіДЫЪБmЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉmЃН3ЁЂ1Лђ
ЃЛЃЈ3ЃЉmЃН3ЁЂ1Лђ![]()
ЁОНтЮіЁП
(1)НЋЕуP(mЃЌn)ДњШыЗДБШР§КЏЪ§y=![]() (xЃО0)ЃЌгУmБэЪОГіnМДПЩБэЪОГіЕуPЕФзјБъЃЌШЛКѓИљОнPAЁЮxжсЃЌЕУЕНAЕуЕФзнзјБъЮЊ
(xЃО0)ЃЌгУmБэЪОГіnМДПЩБэЪОГіЕуPЕФзјБъЃЌШЛКѓИљОнPAЁЮxжсЃЌЕУЕНAЕуЕФзнзјБъЮЊ![]() ЃЌШЛКѓНЋЕуAЕФзнзјБъДјШЫЗДБШР§КЏЪ§ЕФНтЮіЪНy=
ЃЌШЛКѓНЋЕуAЕФзнзјБъДјШЫЗДБШР§КЏЪ§ЕФНтЮіЪНy=![]() (xЃО0)МДПЩЕУЕНЕуAЕФзјБъЃЌЭЌРэЕУЕНЕуBЕФзјБъЃЛ
(xЃО0)МДПЩЕУЕНЕуAЕФзјБъЃЌЭЌРэЕУЕНЕуBЕФзјБъЃЛ
(2)ИљОнPA=m-![]() ЃЌPB=
ЃЌPB=![]()
![]() =
=![]() ЃЌРћгУSЁїPAB=
ЃЌРћгУSЁїPAB=![]() PAPBМДПЩЕУЕНД№АИЃЛ
PAPBМДПЩЕУЕНД№АИЃЛ
(3)ЗжШ§жжЧщПіЗжБ№ЛГіЭМаЮЃЌНсКЯЦНааЫФБпЕФаджЪНјааЬжТлМДПЩ.
(1)ЁпЕуP(mЃЌn)ЪЧЗДБШР§КЏЪ§yЃН![]() (xЃО0)ЭМЯѓЩЯЕФЖЏЕуЃЌ
(xЃО0)ЭМЯѓЩЯЕФЖЏЕуЃЌ
ЁрnЃН![]() ЃЌ
ЃЌ
ЁрЕуP(mЃЌ![]() )ЃЛ
)ЃЛ
ЁпPAЁЮxжсЃЌ
ЁрAЕуЕФзнзјБъЮЊ![]() ЃЌ
ЃЌ
НЋЕуAЕФзнзјБъДњШыЗДБШР§КЏЪ§ЕФНтЮіЪНyЃН![]() (xЃО0)ЕУЃКxЃН
(xЃО0)ЕУЃКxЃН![]() ЃЌ
ЃЌ
ЁрA(![]() ЃЌ
ЃЌ![]() )ЃЌЭЌРэПЩЕУЃКB(mЃЌ
)ЃЌЭЌРэПЩЕУЃКB(mЃЌ![]() )ЃЛ
)ЃЛ
(2)ЁпPAЃНmЉ![]() ЃН
ЃН![]() ЃЌPBЃН
ЃЌPBЃН![]() Љ
Љ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрSЁїPABЃН![]() PAPBЃН
PAPBЃН![]() ЁС
ЁС![]() ЁС
ЁС![]() ЃН
ЃН![]() ЃЛ
ЃЛ
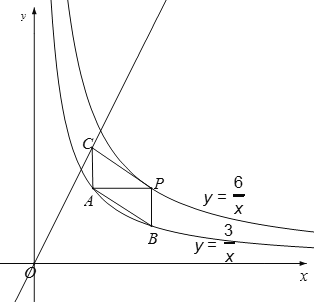
(3)ЂйШєЫФБпаЮPBACЮЊЦНааЫФБпаЮЃЌдђгаACЁЮyжсЃЌ
ЁрCЕуКсзјБъЮЊ![]() ЃЌ
ЃЌ
ДњШыyЃН2xЕУC(![]() ЃЌm)ЃЌ
ЃЌm)ЃЌ
ДЫЪБACЃНmЉ![]() ЃЌPBЃН
ЃЌPBЃН![]() ЃЌ
ЃЌ
гЩACЃНPBЃЌЕУЃКmЉ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
НтЕУЃКmЃН3ЛђmЃНЉ3(ЩсШЅ)ЃЌ
ЁрmЃН3ЪБЃЌЫФБпаЮPBACЮЊЦНааЫФБпаЮЃЎ
ЂкШєЫФБпаЮPABCЮЊЦНааЫФБпаЮЃЌдђгаBCЁЮxжсЃЌ
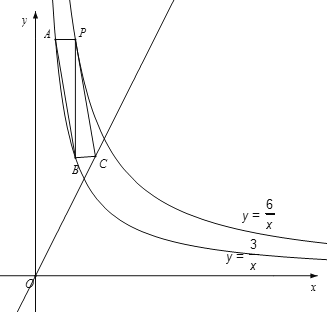
ЁрCЕузнзјБъЮЊ![]() ЃЌ
ЃЌ
АбyЃН![]() ДњШыyЃН2xЕУC(
ДњШыyЃН2xЕУC(![]() ЃЌ
ЃЌ![]() )ЃЌ
)ЃЌ
ДЫЪБBCЃН![]() ЉmЃЌ
ЉmЃЌ
гЩBCЃНPAЃЌЕУ![]() ЉmЃН
ЉmЃН![]() ЃЌ
ЃЌ
НтЕУЃКmЃН1ЛђmЃНЉ1(ЩсШЅ)ЃЛ
ЂлШєPACBЮЊЦНааЫФБпаЮЃЌдђгаACЁЮBPЁЮyжсЃЌ
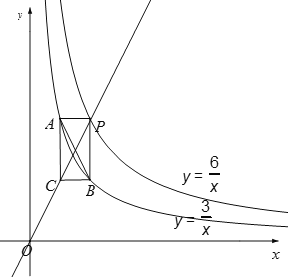
ЁрЕуC(![]() ЃЌ
ЃЌ![]() )ЃЌ
)ЃЌ
ДњШыyЃН2xЃЌЕУ![]() ЃН2ЁС
ЃН2ЁС![]() ЃЌ
ЃЌ
НтЕУmЃН![]() ЛђmЃНЉ
ЛђmЃНЉ![]() (ЩсШЅ)ЃЌ
(ЩсШЅ)ЃЌ
злЩЯЃКmЃН3ЁЂ1Лђ![]() ЪБЃЌвдЕуPЃЌAЃЌBЃЌCЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮ.
ЪБЃЌвдЕуPЃЌAЃЌBЃЌCЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮ.

 ЧсЫЩПЮЬУЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ
ЧсЫЩПЮЬУЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИЁОЬтФПЁПЮЊСЫНтЩЯвЛДЮАЫФъМЖЪ§бЇВтбщГЩМЈЧщПіЃЌЫцЛњГщШЁСЫ40УћбЇЩњЕФГЩМЈНјааЭГМЦЗжЮіЃЌет40УћбЇЩњЕФГЩМЈЪ§ОнШчЯТЃК
55 62 67 53 58 83 87 64 68 85
60 94 81 98 51 83 78 77 66 71
91 72 63 75 88 73 52 71 79 63
74 67 78 61 97 76 72 77 79 71
ЃЈ1ЃЉНЋбљБОЪ§ОнЪЪЕБЗжзщЃЌжЦзїЦЕЪ§ЗжВМБэЃК
Зж зщ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ |
ЦЕ Ъ§ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ |
ЃЈ2ЃЉИљОнЦЕЪ§ЗжВМБэЃЌЛцжЦЦЕЪ§жБЗНЭМЃК
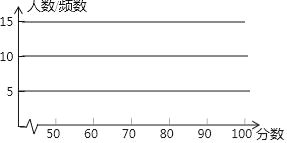
ЃЈ3ЃЉДгЭМПЩвдПДГіЃЌет40УћбЇЩњЕФГЩМЈЖМЗжВМдкЪВУДЗЖЮЇФкЃПЗжЪ§дкФФИіЗЖЮЇЕФШЫЪ§зюЖрЃП