题目内容
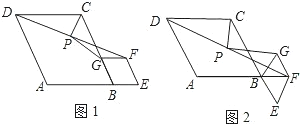
 如图①,在菱形ABCD中,动点P从点B出发,沿折线B→C→D→B运动.设点P经过的路程为x,△ABP的面积为y.把y看作x的函数,函数的图象如图②所示,则图②中的b等于
如图①,在菱形ABCD中,动点P从点B出发,沿折线B→C→D→B运动.设点P经过的路程为x,△ABP的面积为y.把y看作x的函数,函数的图象如图②所示,则图②中的b等于
- A.

- B.

- C.5
- D.4
B
分析:连接AC交BD于O,根据图②求出菱形的边长为4,对角线BD为6,根据菱形的对角线互相垂直平分求出BO,再利用勾股定理列式求出CO,然后求出AC的长,再根据菱形的面积等于对角线乘积的一半求出菱形的面积,b为点P在CD上时△ABP的面积,等于菱形的面积的一半,从而得解.
解答: 解:如图,连接AC交BD于O,
解:如图,连接AC交BD于O,
由图②可知,BC=CD=4,BD=14-8=6,
∴BO= BD=
BD= ×6=3,
×6=3,
在Rt△BOC中,CO= =
= =
= ,
,
AC=2CO=2 ,
,
所以,菱形的面积= AC•BD=
AC•BD= ×2
×2 ×6=6
×6=6 ,
,
当点P在CD上运动时,△ABP的面积不变,为b,
所以,b= ×6
×6 =3
=3 .
.
故选B.
点评:本题考查了动点问题的函数图象,主要利用了菱形的对角线互相垂直平分的性质,菱形的面积等于对角线乘积的一半,根据图形得到菱形的边长与对角线BD的长是解题的关键.
分析:连接AC交BD于O,根据图②求出菱形的边长为4,对角线BD为6,根据菱形的对角线互相垂直平分求出BO,再利用勾股定理列式求出CO,然后求出AC的长,再根据菱形的面积等于对角线乘积的一半求出菱形的面积,b为点P在CD上时△ABP的面积,等于菱形的面积的一半,从而得解.
解答:
 解:如图,连接AC交BD于O,
解:如图,连接AC交BD于O,由图②可知,BC=CD=4,BD=14-8=6,
∴BO=
 BD=
BD= ×6=3,
×6=3,在Rt△BOC中,CO=
 =
= =
= ,
,AC=2CO=2
 ,
,所以,菱形的面积=
 AC•BD=
AC•BD= ×2
×2 ×6=6
×6=6 ,
,当点P在CD上运动时,△ABP的面积不变,为b,
所以,b=
 ×6
×6 =3
=3 .
.故选B.
点评:本题考查了动点问题的函数图象,主要利用了菱形的对角线互相垂直平分的性质,菱形的面积等于对角线乘积的一半,根据图形得到菱形的边长与对角线BD的长是解题的关键.

练习册系列答案
相关题目
 原问题中的其他条件不变,请你直接写出
原问题中的其他条件不变,请你直接写出


