题目内容
 如图所示,甲,乙两船同时从港口出发,甲船以16.1海里/小时的速度向南偏东58°方向航行,乙船向南偏西32°方向航行,航行了2小时,甲船到达A处并观测到B处的乙船恰好在其正西方向,则乙船的速度为
如图所示,甲,乙两船同时从港口出发,甲船以16.1海里/小时的速度向南偏东58°方向航行,乙船向南偏西32°方向航行,航行了2小时,甲船到达A处并观测到B处的乙船恰好在其正西方向,则乙船的速度为分析:有时间2小时,求速度,需要知道距离即OB,由题可知△ABO为直角三角形,利用∠A的正切值以及OA的长,即可解决.
解答:解:由题意可得OA=16.1×2=32.2(海里).
∠1=58°,∠2=32°,
∴∠AOB=∠1+∠2=90°.
∵B在A的正西方向,
∴∠A=32°.
又∵在Rt△AOB中,tanA=
,
∴OB=OA•tanA=32.2×tan32°≈32.2×0.624≈20.1
∴v=
=
=10.05≈10.1(海里/小时).
即乙船的速度是10.1海里/小时.
故答案为:10.1.
∠1=58°,∠2=32°,
∴∠AOB=∠1+∠2=90°.
∵B在A的正西方向,
∴∠A=32°.
又∵在Rt△AOB中,tanA=
| OB |
| OA |
∴OB=OA•tanA=32.2×tan32°≈32.2×0.624≈20.1
∴v=
| OB |
| 2 |
| 20.1 |
| 2 |
即乙船的速度是10.1海里/小时.
故答案为:10.1.
点评:解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 小时后再转向正东北方向开往B岛,其速度仍为20海里/小时.
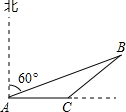
小时后再转向正东北方向开往B岛,其速度仍为20海里/小时. (2013•徐州模拟)如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,停留半小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.
(2013•徐州模拟)如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,停留半小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.
