题目内容
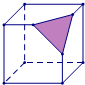（2012•房山区二模）过正方体中有公共顶点的三条棱的中点切出一个平面，形成如图几何体，其正确展开图为（ ）分析：由平面图形的折叠及立体图形的表面展开图的特点解题．
解答：解：选项A、C、D折叠后都不符合题意，只有选项B折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点，与正方体三个剪去三角形交于一个顶点符合．
故选B．
故选B．
点评：考查了截一个几何体和几何体的展开图．解决此类问题，要充分考虑带有各种符号的面的特点及位置．
练习册系列答案
相关题目
