题目内容
如图，△ABC是边长为2的等边三角形，点E、F分别在CB和BC的延长线上，且∠EAF=120°，设BE=x，CF=y．求y与x的函数关系，并画出这个函数的图象．
解：∵∠EAF=120°，∠BAC=60°
∴∠EAB+∠CAF=60°
∵∠EAB+∠E=∠ABC=60°
∴∠E=∠CAF
∵∠EBA=∠ACF=120°
∴△EBA∽△CAF
∴EB：AC=BA：CF
∴x：2=2：y，
∴y=
（x＞0）．
作图如下：
分析：由已知可推出∠E=∠CAF，根据外角的性质可得∠EBA=∠ACF，从而可判定△EBA∽△ACF，根据相似三角形的对应边对应成比例即可表示出x与y的关系，从而不难求解．
点评：此题主要考查学生对相似三角形的判定与性质及反比例函数的实际运用能力，同时考查了等边三角形的性质．
∴∠EAB+∠CAF=60°
∵∠EAB+∠E=∠ABC=60°
∴∠E=∠CAF
∵∠EBA=∠ACF=120°
∴△EBA∽△CAF
∴EB：AC=BA：CF
∴x：2=2：y，
∴y=
（x＞0）．作图如下：
分析：由已知可推出∠E=∠CAF，根据外角的性质可得∠EBA=∠ACF，从而可判定△EBA∽△ACF，根据相似三角形的对应边对应成比例即可表示出x与y的关系，从而不难求解．
点评：此题主要考查学生对相似三角形的判定与性质及反比例函数的实际运用能力，同时考查了等边三角形的性质．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
如图，△ABC是边长为a的等边三角形，O为△ABC的中心．将△ABC绕着中心O旋转120°．
点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．
（2013•溧水县一模）如图，△ABC是边长为4的等边三角形，将△ABC沿直线BC向右平移，使B点与C点重合，得到△DCE，连结BD，交AC于F．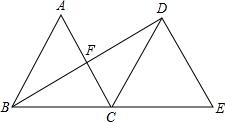
（2012•湘潭）如图，△ABC是边长为3的等边三角形，将△ABC沿直线BC向右平移，使B点与C点重合，得到△DCE，连接BD，交AC于F．
如图，△ABC是边长为3的等边三角形，△BDC是等腰三角形，且∠BDC=120°，以D为顶点做一个60°角，使其两边分别交AB于点M，交AC于点N，连接MN，则△AMN的周长为