题目内容
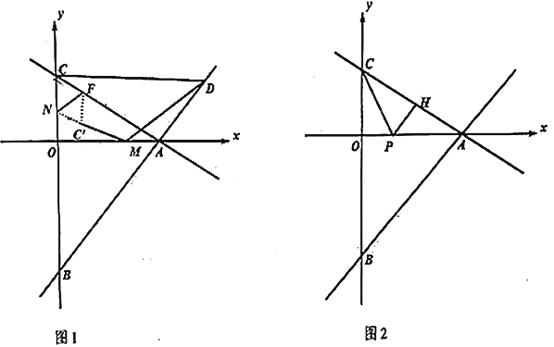
【题目】如图1，已知直线
和直线
交于
轴上一点
，且分别交
轴于点
、点
，且
.
（1）求
的值；
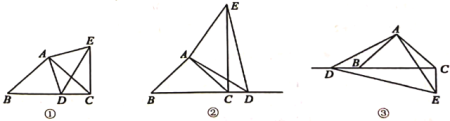
（2）如图1，点
是直线
上一点，且在轴上方，当
时，在线段
上取一点
，使得
，点
分别为轴、轴上的动点，连接
，将
沿翻折至
，求
的最小值；
（3）如图2，
分别为射线
上的动点，连接
是否存在这样的点
，使得
为等腰三角形，
为直角三角形同时成立.请直接写出满足条件的点坐标.
【答案】（1）
；（2）
；（3）
或
或
【解析】
（1）首先由已知得出点B和C的坐标，即可得出直线AC的解析式，然后得出点A的坐标，代入直线AB，即可得出
的值；
（2）首先根据△ACD的面积求出点D坐标，然后由
得出点F的坐标和CF，若使
有最小值,则M、C′、D在一条直线上，作F和C′关于
轴的对称点F′和C′′，根据D和F′的坐标得出DF′，然后即可得解；
（3）若使得
为等腰三角形，
为直角三角形同时成立，则分情况求解，H在AC上和AC的延长线上，根据平行线成比例和相似三角形的性质，列出方程，即可得出P坐标.
（1）由已知，得
∵
，C在轴正半轴，B在轴负半轴
∴
即
∴直线
，直线
∴
，将其代入直线AB，
∴
（2）∵点
是直线
上一点，设点D坐标为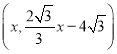
∴
即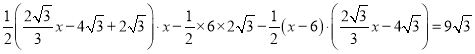
∴
，即D
∵
∴
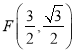,即C′在以CF为半径的圆上，
若使有最小值,则M、C′、D在一条直线上，作F和C′关于轴的对称点F′和C′′，如图所示，则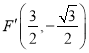
，
∴
∴
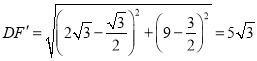
（3）根据题意，分情况求解：
①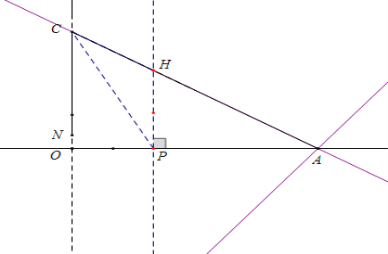
若PH⊥OA，则HP=HC，HP∥CN
∴
设H（x，y）可得
,
∴
②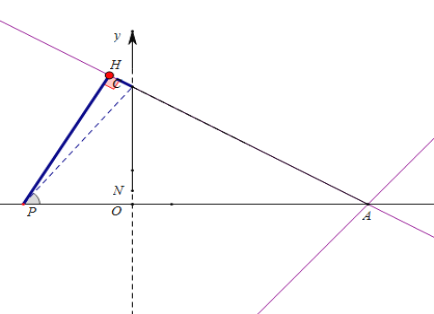
若PH⊥AC，则HP=HC，
∴△APH∽△ACO
∴
设
，可得
∴
∴
∴
③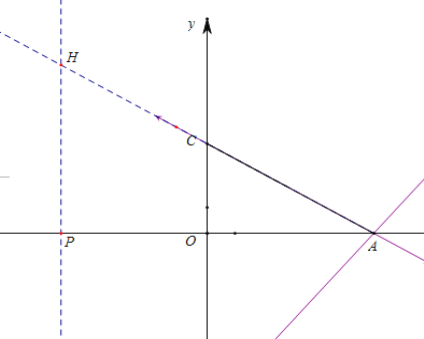
若PH⊥OA，∠H=∠ACO=60°
∴HP=HC=PC
∴
设H（x，y）可得
∴
故满足条件的点P坐标为或或.
同步练习强化拓展系列答案
【题目】学校在八年级新生中举行了全员参加的数学应用能力大赛，试卷题目共10题，每题10分.现分别从三个班中各随机取10名同学的成绩（单位：分），收集数据如下：
1班：90，70，80，80，80，80，80，90，80，100；
2班：70，80，80，80，60，90，90，90，100，90；
3班：90，60，70，80，80，80，80，90，100，100.
整理数据：
人数 班级 | 60分人数 | 70分人数 | 80分人数 | 90分人数 | 100分人数 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
平均数 | 中位数 | 众数 | |
83 | 80 | 80 | |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
分析数据：
根据以上信息回答下列问题：
（1）请直接写出表格中
，
，
，
的值；
（2）比较这三组样本数据的平均数、中位数和众数，你认为哪个班的成绩比较好？请说明理由（写两条支持你结论的理由）.
