题目内容
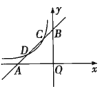
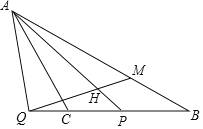
【题目】如图，把
绕着点
顺时针方向旋转角度
（
），得到
，若
，
，
三点在同一条直线上，
，则的度数是___________．
【答案】
【解析】
首先根据邻补角定义求出∠BCC′=180°-∠BCB′=134°，再根据旋转的性质得出∠BCA=∠C′，AC=AC′，根据等边对等角进一步可得出∠BCA=∠ACC′=∠C′，再利用三角形内角和求出∠CAC′的度数，从而得出α的度数．．
解：∵B，C，C′三点在同一条直线上，∴∠BCC′=180°-∠BCB′=134°，
又根据旋转的性质可得，
∠CAC′=∠BAB′=α，∠BCA=∠C′，AC=AC′，
∴∠ACC′=∠C′，
∴∠BCA=∠ACC′=
∠BCC′=67°=∠C′，
∴∠CAC′=180°-∠ACC′-∠C′=46°，
∴α=46°．
故答案为：46°．
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体，并用流量、速度、密度三个概念描述车流的基本特征，其中流量
（辆
小时）指单位时间内通过道路指定断面的车辆数；速度
（千米小时）指通过道路指定断面的车辆速度，密度
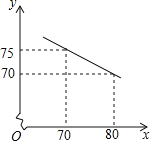
（辆千米）指通过道路指定断面单位长度内的车辆数．为配合大数据治堵行动，测得某路段流量与速度之间关系的部分数据如下表：
速度v（千米/小时） |
|
|
|
|
|
|
|
|
流量q（辆/小时） |
|
|
|
|
|
|
|
|
（1）根据上表信息，下列三个函数关系式中，刻画，关系最准确是_____________________．（只填上正确答案的序号）
①
；②
；③
（2）请利用（1）中选取的函数关系式分析，当该路段的车流速度为多少时，流量达到最大？最大流量是多少？
（3）已知，，满足
，请结合（1）中选取的函数关系式继续解决下列问题：市交通运行监控平台显示，当
时道路出现轻度拥堵．试分析当车流密度在什么范围时，该路段将出现轻度拥堵？
【题目】一家游泳馆的游泳收费标准为30元/次，若购买会员年卡，可享受如下优惠：
会员年卡类型 | 办卡费用（元） | 每次游泳收费（元） |
A 类 | 50 | 25 |
B 类 | 200 | 20 |
C 类 | 400 | 15 |
例如，购买A类会员年卡，一年内游泳20次，消费50+25×20＝550元，若一年内在该游泳馆游泳的次数介于40～50次之间，则最省钱的方式为（ ）
A.购买A类会员卡B.购买B类会员年卡
C.购买C类会员年卡D.不购买会员年卡