题目内容
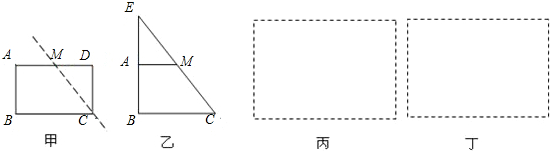
如图(一)所示的纸片是半径为10cm的圆形纸片的一部分,且弦AB的长为 cm.
cm.
(1)请你用直尺、圆规找出该圆的圆心O,并求弦AB所对的圆心角的度数;
(2)请问能否利用该纸片制作出如图(二)所示的无底冰淇淋纸筒,并说明理由.
(注:①保留作图痕迹,并用0.5黑水笔描粗;②图(2)中的冰淇淋纸筒的尺寸为:底面直径为12cm,高为8cm)

 (1)如图所示
(1)如图所示过点O作OC⊥AB于C,连接OA,OB,

∴AC=
 AB=5
AB=5 ,
,∵OA=10,
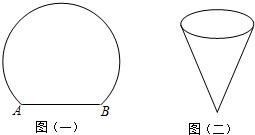
∴sin∠AOC=
 =
= ,
,∴∠AOC=60°,
∴∠AOB=120°;
(2)如图示,
由(1)得:弧长为:
 =
= ,
,用如图所示的扇形制成圆锥,
圆锥的底面圆周长为:
 ,
,所以底面圆的半径为r=
 (cm).
(cm).而图二所示的圆锥要求底面圆的半径为6cm,
所以能制成所要求的无底冰淇淋纸筒.
分析:(1)画出图形如图示.
(2)能,因为无底冰淇淋纸筒是圆锥,
点评:本题既考查了垂径定理,即根据垂径定理的推论来确定圆心,又考查了平面图形与立体图形之间的转化知识--圆锥,在解题时把平面图形与立体图形结合起来是解题的关键.

练习册系列答案
相关题目
 cm.
cm.