��Ŀ����
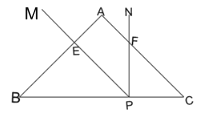
����Ŀ����ͼ����֪![]() �У�
�У�![]() ���ף�
���ף�![]() ���ף���
���ף���![]() Ϊ
Ϊ![]() ���е㣮
���е㣮
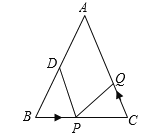
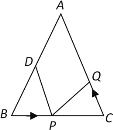
��1�������P���߶�BC����3����/����ٶ���B����C���˶���ͬʱ����Q���߶�CA����C����A���˶���
������Q���˶��ٶ����P���˶��ٶ���ȣ�����1���![]() ��
��![]() �Ƿ�ȫ�ȣ���˵�����ɣ�
�Ƿ�ȫ�ȣ���˵�����ɣ�
������Q���˶��ٶ����P���˶��ٶȲ���ȣ� ![]() ��
��![]() �Ƿ����ȫ�ȣ����ܣ����ȫ��ʱ��Q���˶��ٶȺ�ʱ�䣻�����ܣ���˵�����ɣ�
�Ƿ����ȫ�ȣ����ܣ����ȫ��ʱ��Q���˶��ٶȺ�ʱ�䣻�����ܣ���˵�����ɣ�
��2������Q�Ԣ��е��˶��ٶȴӵ�C��������P��ԭ�����˶��ٶȴӵ�Bͬʱ����������ʱ����![]() �����˶������ʱ���P���Q��һ����
�����˶������ʱ���P���Q��һ����![]() ����������������
����������������
���𰸡���1����![]() �����ɼ���������
�����ɼ���������![]() �룬
�룬![]() ����/�룻��2������
����/�룻��2������![]() �룬��
�룬��![]() ���
���![]() ��һ���ڱ�
��һ���ڱ�![]() ������
������
��������
��1���ٸ��ݡ�·��=�ٶȡ�ʱ�䡱�ɵ�![]() ��Ȼ��֤��
��Ȼ��֤��![]() �����ݵȱ߶ԵȽ�֤��
�����ݵȱ߶ԵȽ�֤��![]() ���������SAS����֤�����ۣ�
���������SAS����֤�����ۣ�
�ڸ�������ɵ�![]() ,��
,��![]() ��
��![]() ȫ�ȣ���
ȫ�ȣ���![]() �����ݡ�·�̡��ٶ�=ʱ�䡱�������P���˶�ʱ�䣬��Ϊ��Q�˶���ʱ�䣬Ȼ�������Q���ٶȣ�
�����ݡ�·�̡��ٶ�=ʱ�䡱�������P���˶�ʱ�䣬��Ϊ��Q�˶���ʱ�䣬Ȼ�������Q���ٶȣ�
��2���辭��![]() ����
����![]() ���
���![]() ��һ����������������ɵõ�
��һ����������������ɵõ�![]() ���
���![]() ��һ������ʱ����Q�ȵ�P����AB��AC=20���ף��г����̣������������ʱ�䣬�Ӷ������P�˶���·�̣��Ӷ��жϳ����ۣ�
��һ������ʱ����Q�ȵ�P����AB��AC=20���ף��г����̣������������ʱ�䣬�Ӷ������P�˶���·�̣��Ӷ��жϳ����ۣ�
�⣺��1���١�![]() �룬
�룬
��![]() ���ף�
���ף�
��![]() ���ף���
���ף���![]() Ϊ
Ϊ![]() ���е㣬
���е㣬
��![]() ���ף�
���ף�
�֡�![]() ���ף�
���ף�
��![]() ���ף�
���ף�
��![]() ��
��
�֡�![]() ��
��
��![]() ��
��
�ڡ�BPD�͡�CQP��
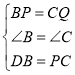
��![]() ��
��
�ڡ�![]() ��
��
��![]() ��
��
�֡�![]() ��
��![]() ȫ�ȣ�
ȫ�ȣ�
![]() ��
��
��![]() ��
��
���![]() ����
����![]() �˶���ʱ��
�˶���ʱ��![]()
![]() �룬
�룬
��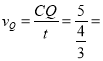
![]() ����/�룮
����/�룮
��2���辭��![]() ����
����![]() ���
���![]() ��һ��������
��һ��������
��![]()
���![]() ���
���![]() ��һ������ʱ����Q�ȵ�P����AB��AC=20����
��һ������ʱ����Q�ȵ�P����AB��AC=20����
��![]() ��
��
���![]() �룮
�룮
���![]() ���˶���
���˶���![]() ���ף�
���ף�
��![]() ��
��
���![]() ����
����![]() ��
��![]() ����������
����������
�ྭ��![]() �룬��
�룬��![]() ���
���![]() ��һ���ڱ�
��һ���ڱ�![]() ��������
��������

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�