题目内容
 (2013•牡丹江)如图,△ABO中,AB⊥OB,OB=
(2013•牡丹江)如图,△ABO中,AB⊥OB,OB=| 3 |
分析:需要分类讨论:在把△ABO绕点O顺时针旋转150°和逆时针旋转150°后得到△A1B1O时点A1的坐标.
解答: 解:∵△ABO中,AB⊥OB,OB=
解:∵△ABO中,AB⊥OB,OB=
,AB=1,
∴tan∠AOB=
=
,
∴∠AOB=30°.
如图1,当△ABO绕点O顺时针旋转150°后得到△A1B1O,则∠A1OC=150°-∠AOB-∠BOC=150°-30°-90°=30°,
则易求A1(-1,-
);
如图2,当△ABO绕点O逆时针旋转150°后得到△A1B1O,则∠A1OC=150°-∠AOB-∠BOC=150°-30°-90°=30°,
则易求A1(-2,0);
综上所述,点A1的坐标为(-,-
)或(-2,0);
故选B.
 解:∵△ABO中,AB⊥OB,OB=
解:∵△ABO中,AB⊥OB,OB=| 3 |
∴tan∠AOB=
| AB |
| OB |
| ||
| 3 |
∴∠AOB=30°.
如图1,当△ABO绕点O顺时针旋转150°后得到△A1B1O,则∠A1OC=150°-∠AOB-∠BOC=150°-30°-90°=30°,
则易求A1(-1,-
| 3 |
如图2,当△ABO绕点O逆时针旋转150°后得到△A1B1O,则∠A1OC=150°-∠AOB-∠BOC=150°-30°-90°=30°,
则易求A1(-2,0);
综上所述,点A1的坐标为(-,-
| 3 |
故选B.
点评:本题考查了坐标与图形变化--旋转.解题时,注意分类讨论,以防错解.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
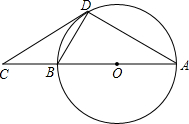 (2013•牡丹江)如图,点C是⊙O的直径AB延长线上的一点,且有BO=BD=BC.
(2013•牡丹江)如图,点C是⊙O的直径AB延长线上的一点,且有BO=BD=BC.