��Ŀ����
����Ŀ��ijУ���Ż���������ѡ���У�����A��������B��������C������ë��D����ƹ����E����ÿ��ѧ��ѡ�����е�һ�ţ�ѧУ��ij��ȫ��ͬѧ��ѡ��������е���ͳ�ƺ��Ƴ�����������ͳ��ͼ�� 
��1����������ð��������������ȫƵ���ֲ�ֱ��ͼ��
��2���ð������ij4��ͬѧ��1��ѡ������A����2��ѡ������B����1��ѡ������C������Ҫ����4����ѡ2�ˣ��������б�����״ͼ�ķ�������ѡ����2��ǡ��1��ѡ������1��ѡ������ĸ��ʣ�
���𰸡�
��1���⣺������=12��24%=50���ˣ���E������=50��10%=5���ˣ���
����A������=50��7��12��9��5=17���ˣ���
Ƶ���ֲ�ֱ��ͼΪ��
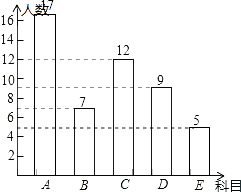
��2���⣺�б����£�
��һ����ѡ�� �ڶ�����ѡ�� | A | B | B | C |
A | AB | AB | AC | |
B | AB | BB | BC | |
B | AB | BB | BC | |
C | AC | BC | BC |
����12�ֵȿ��ܵĽ����������ѡ����2��ǡ��1��ѡ������1��ѡ������Ľ����Ϊ4��
����ѡ����2��ǡ��1��ѡ������1��ѡ������ĸ���= ![]() =
= ![]()
����������1������A���������������ռ�İٷֱȼ��ɵõ����������ټ����E��������Ȼ������A��������ȫƵ���ֲ�ֱ��ͼ����2�������б���չʾ����12�ֵȿ��ܵĽ���������ҳ�ѡ����2��ǡ��1��ѡ������1��ѡ������Ľ������Ȼ����ݸ��ʹ�ʽ��⣮
�����㾫��������Ƶ���ֲ�ֱ��ͼ���б�������״ͼ���ǽ����ĸ�������Ҫ֪���ص㣺��������ʾ�����Ƶ���ֲ��������������ʾ�����Ƶ����𣮣�ע����������ͳ��ͼ��Ƶ���ֲ�ֱ��ͼ������һ������Ҫ�����������������ʱ�����б����Ͳ������ˣ�Ϊ�˲��ز�©���г����п��ܵĽ����ͨ��������״ͼ������ʣ�

����Ŀ��ij����Ʒ�������һ��ɱ�Ϊ10Ԫ/����С����ƷͶ���г������������������飬�õ��������ݣ� 
���۵���x��Ԫ/���� | �� | 20 | 30 | 40 | 50 | 60 | �� |
ÿ��������y������ | �� | 500 | 400 | 300 | 200 | 100 | �� |
��1�����ϱ���x��y�ĸ����Ӧֵ��Ϊ������꣬�������ƽ��ֱ������ϵ�������Ӧ�ĵ㣬����y��x�ĺ�����ϵ�������������ϵʽ��
��2�������۵���Ϊ����Ԫʱ������Ʒ��������С����Ʒÿ���õ����������������Ƕ��٣�������=���۶�ɱ���







