题目内容
11.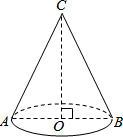 如图,一个圆锥形漏斗的底面半径OB=6cm,高OC=8cm.则这个圆锥漏斗的侧面积是( )
如图,一个圆锥形漏斗的底面半径OB=6cm,高OC=8cm.则这个圆锥漏斗的侧面积是( )| A. | 30cm2 | B. | 30πcm2 | C. | 60πcm2 | D. | 120cm2 |
分析 先利用勾股定理计算出圆锥的母线长,然后利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式计算这个圆锥漏斗的侧面积.
解答 解:圆锥的母线长=$\sqrt{{6}^{2}+{8}^{2}}$=10,
所以圆锥的侧面积=$\frac{1}{2}$•2π•6•10=60π(cm2).
故选C.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB等于( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB等于( )
 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB等于( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB等于( )| A. | 70° | B. | 20° | C. | 140° | D. | 35° |
16. 如图,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
 如图,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )| A. | $\frac{15\sqrt{3}}{4}$-$\frac{3}{2}π$ | B. | $\frac{15\sqrt{3}}{2}$-$\frac{3}{2}π$ | C. | $\frac{7\sqrt{3}}{4}$-$\frac{π}{6}$ | D. | $\frac{7\sqrt{3}}{2}$-$\frac{π}{6}$ |
20.一组数据1,8,5,3,3的中位数是( )
| A. | 3 | B. | 3.5 | C. | 4 | D. | 5 |
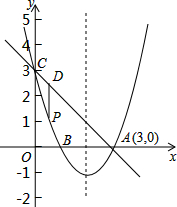 如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.
如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.
 如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm. 如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.
如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.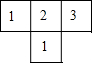 如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中数字表示该位置小正方体的个数,则该几何体的左视图是( )
如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中数字表示该位置小正方体的个数,则该几何体的左视图是( )