题目内容
【题目】已知, ![]() 、
、![]() 均为等边三角形,点
均为等边三角形,点![]() 是
是![]() 内的点
内的点
(1)如图①,说明![]() 的理由;
的理由;

(2)如图②,当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 的度数;
的度数;

(3)当![]() 为等腰直角三角形时,
为等腰直角三角形时,![]() ________度(直接写出客案).
________度(直接写出客案).
【答案】(1)见解析;(2)见解析;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先理由等边三角形的性质得出![]() ,
,![]() ,
,![]() ,即可得出结论;
,即可得出结论;
(2)同(1)得![]() ,再判断出
,再判断出![]() ,进而求出
,进而求出![]() ,即可得出结论;
,即可得出结论;
(3)当![]() 为等腰直角三角形时,有三种情况:I.当∠EDB=90°,DE=DB时, II.当∠BED=90°,BE=DB时,当∠EDB=90°,DE=DB时,分别作出图形,然后根据等腰三角形性质即可求出.
为等腰直角三角形时,有三种情况:I.当∠EDB=90°,DE=DB时, II.当∠BED=90°,BE=DB时,当∠EDB=90°,DE=DB时,分别作出图形,然后根据等腰三角形性质即可求出.
解:(1)∵![]() 和
和![]() 都是等边三角形(已知)
都是等边三角形(已知)
∴![]() ,
,![]() ,
,![]() (等边三角形的性质)。
(等边三角形的性质)。
∴![]() (等式性质),即
(等式性质),即![]() ,
,
在![]() 和
和![]() 中,
中,
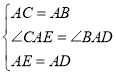 ,
,
∴![]()
∴![]() (全等三角形对应边相等)
(全等三角形对应边相等)
(2)∵![]() 是等边三角形(已知)。
是等边三角形(已知)。
∴![]() (等边三角形的性质)。
(等边三角形的性质)。
∴![]() (邻补角的意义)
(邻补角的意义)
∴![]() (等式性质)
(等式性质)
∴同理(1)得![]()
∴![]() (全等三角形对应角相等)
(全等三角形对应角相等)
∴![]() (等式性质)
(等式性质)
(3)当![]() 为等腰直角三角形时,有三种情况:
为等腰直角三角形时,有三种情况:
I.当∠EDB=90°,DE=DB时,如图③-1:

∵∠ADE=60°,
∴∠ADB=∠ADE+∠EDB=60°+90°=150°,
又∵AD=DE,
∴AD=BD,
∴∠DAB=∠ABD=![]() ;
;
II.当∠BED=90°,BE=DB时,如图③-2:
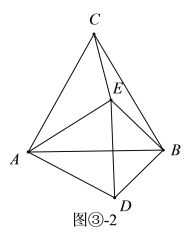
在△ABE和△ADB中:
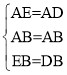 ,
,
∴△ABE≌△ADB(SSS)
∴∠ABE=∠ABD,
∴ ![]() ;
;
III.当∠EDB=90°,DE=DB时,如图③-3:

同I可得:∠ABE=15°,
∵∠EBD=![]() ,
,
∴∠ABD=![]() .
.
综上所述:∠ABD=![]() 或
或![]() 或
或![]() .
.
故答案为:![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目