Question

已知⊙O的半径为R，PA，PB为⊙O的切线，M为AB延长线上一点，N为OM上一点，且OM•OM=R²，求证：PN⊥OM．

Answer 1

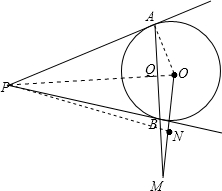证明：连接OA，则OM•ON=OA²，
连接OP，交AB于Q，连接PN，则OP⊥AQ，
∵在Rt△PAO中，AQ为底边PO上的高，
∴∠PAO=∠AQO=90°，又∠AOQ=∠POA，
∴△AOQ∽△POA，
∴，
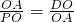∴OA²=OQ•OP，
∴OM•ON=OQ•OP，即=，
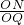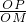又∠PON=∠MOQ，
∴△PON∽△MOQ，
∴∠PNO=∠MQO=90°，
∴PN⊥OM．
分析：连接OA，由切线性质得到OA与AP垂直，OA为圆的半径，则有ON•OM=OA²，再连接OP，根据切线长定理得到PO与AB垂直，根据一对公共角及一对直角相等得到三角形AOD与三角形APO相似，根据相似得比例可得OA²=OP•OQ，等量代换得到OMON=OPOQ，又根据一对公共角，利用两边对应成比例且夹角相等的两三角形相似，可得三角形OQM与三角形OPN相似，根据相似三角形的对应角相等，可得∠PNO=∠OQM=90°，得证．
点评：此题考查了切线的性质，相似三角形的判定与性质，以及切线长定理，遇到直线与圆相切问题时，常常连接圆心与切点，构造直角三角形解决问题，切线长定理为经过圆外一点作圆的两条切线，切线长相等，此点与圆心的连线平分两切线的夹角，且与两切点的连线垂直，根据题意画出相应的图形，灵活运用相似三角形的判定与性质是解本题的关键．