题目内容
阅读材料:
为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,设x2-1=y,
则原方程可化为y2-5y+4=0,①
解得y1=1,y2=4.
当y=1时,x2-1=1,∴x2=2即x= 。
。
当y=4时,x2-1=4,∴x2=5即x= 。
。
∴原方程的解为x1= ,x2=
,x2= ,x3=
,x3= ,x4=
,x4= 。
。
根据以上材料,解答下列问题。
(1)填空:在原方程得到方程①的过程中,利用换元法达到降次的目的,体现了_____的数学思想。
(2)解方程x4-x2-6=0。
为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,设x2-1=y,
则原方程可化为y2-5y+4=0,①
解得y1=1,y2=4.
当y=1时,x2-1=1,∴x2=2即x=
 。
。当y=4时,x2-1=4,∴x2=5即x=
 。
。∴原方程的解为x1=
 ,x2=
,x2= ,x3=
,x3= ,x4=
,x4= 。
。根据以上材料,解答下列问题。
(1)填空:在原方程得到方程①的过程中,利用换元法达到降次的目的,体现了_____的数学思想。
(2)解方程x4-x2-6=0。
解:(1)转化。
(2)设 ,
,
则原方程可化为 。
。
解得 (不合题意,舍去)。
(不合题意,舍去)。
由 可得解是:
可得解是: ,
,
故方程 的解是
的解是 。
。
(2)设
 ,
,则原方程可化为
 。
。解得
 (不合题意,舍去)。
(不合题意,舍去)。由
 可得解是:
可得解是: ,
,故方程
 的解是
的解是 。
。
练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
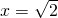 ;
;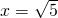 ,
,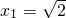 ,
, ,
,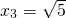 ,
,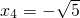 .
. ;
; ,
, ,x2=
,x2= ,x3=
,x3= ,x4=
,x4= .
.