题目内容
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示
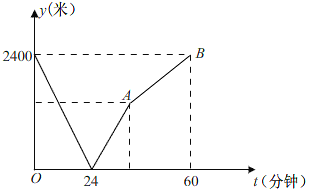
(1)根据图象信息,当t= 分钟时甲乙两人相遇,甲的速度为 米/分钟;
(2)求出线段AB所表示的函数表达式
(3)甲、乙两人何时相距400米?
【答案】(1)24,40;(2)y=40t(40≤t≤60);(3)出发20分钟或28分钟后,甲、乙两人何时相距400米
【解析】
(1)根据图象信息,当t=24分钟时甲乙两人相遇,甲60分钟行驶2400米,根据速度=路程÷时间可得甲的速度;
(2)由t=24分钟时甲乙两人相遇,可得甲、乙两人的速度和为2400÷24=100米/分钟,减去甲的速度得出乙的速度,再求出乙从图书馆回学校的时间即A点的横坐标,用A点的横坐标乘以甲的速度得出A点的纵坐标,再将A、B两点的坐标代入,利用待定系数法即可求出线段AB所表示的函数表达式;
(3)分相遇前后两种情况列方程解答即可.
解:(1)根据图象信息,当t=24分钟时甲乙两人相遇,甲的速度为2400÷60=40(米/分钟).
故答案为24,40;
(2)∵甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,t=24分钟时甲乙两人相遇,
∴甲、乙两人的速度和为2400÷24=100米/分钟,
∴乙的速度为100﹣40=60(米/分钟).
乙从图书馆回学校的时间为2400÷60=40分钟,
40×40=1600,
∴A点的坐标为(40,1600).
设线段AB所表示的函数表达式为y=kt+b,
∵A(40,1600),B(60,2400),
∴![]() ,解得
,解得![]() ,
,
∴线段AB所表示的函数表达式为y=40t(40≤t≤60);
(3)设出发t分钟后两人相距400米,根据题意得
(40+60)t=2400﹣400或(40+60)t=2400+400,
解得t=20或t=28,
答:出发20分钟或28分钟后,甲、乙两人何时相距400米.