ЬтФПФкШн
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌХзЮяЯпy=Љ ![]() ЃЈxЉhЃЉ2+kгыxжсНЛгкAЁЂBЃЌгыyжсНЛгкCЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЌЖдГЦжсНЛxжсгкHЃЌжБЯпy=
ЃЈxЉhЃЉ2+kгыxжсНЛгкAЁЂBЃЌгыyжсНЛгкCЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЌЖдГЦжсНЛxжсгкHЃЌжБЯпy= ![]() x+
x+ ![]() ОЙ§ЕуAгыЖдГЦжсНЛгкEЃЌЕуEЕФзнзјБъЮЊ3ЃЎ
ОЙ§ЕуAгыЖдГЦжсНЛгкEЃЌЕуEЕФзнзјБъЮЊ3ЃЎ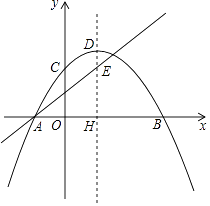
ЃЈ1ЃЉЧѓhЁЂkЕФжЕЃЛ
ЃЈ2ЃЉЕуPЮЊЕкЫФЯѓЯоХзЮяЯпЩЯвЛЕуЃЌСЌНгPHЃЌЕуQЮЊPHЕФжаЕуЃЌСЌНгAQЁЂAPЃЌЩшЕуPЕФКсзјБъЮЊtЃЌЁїAQPЕФУцЛ§ЮЊSЃЌЧѓSгыtЕФКЏЪ§ЙиЯЕЪНЃЈжБНгаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЙ§ЕуQзїyжсЕФЦНааЯпQKЃЌЙ§ЕуDзїyжсЕФДЙжБDKЃЌжБЯпQKЁЂDKНЛгкЕуKЃЌСЌНгPKЁЂEKЃЌШє2ЁЯDKE+ЁЯHPK=90ЁуЃЌЧѓЕуPЕФКсзјБъЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКЁпЕуEЕФзнзјБъЮЊ3ЃЌ
Ёр3= ![]() x+
x+ ![]() ЃЌ
ЃЌ
НтЕУЃКx=2ЃЌ
ЁрDЕуЕФКсзјБъЪЧ2ЃЌ
Ёрh=2ЃЌ
ЁпжБЯпy= ![]() x+
x+ ![]() ОЙ§ЕуAЃЌ
ОЙ§ЕуAЃЌ
ЁрAЃЈЉ2ЃЌ0ЃЉДњШыy=Љ ![]() ЃЈxЉhЃЉ2+kЕУЃЌ0=Љ
ЃЈxЉhЃЉ2+kЕУЃЌ0=Љ ![]() ЃЈЉ2ЉhЃЉ2+kЃЌ
ЃЈЉ2ЉhЃЉ2+kЃЌ
Ёрk=4ЃЛ
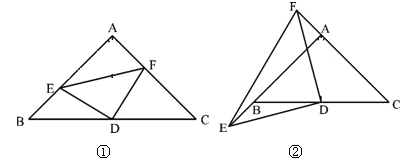
ЃЈ2ЃЉНтЃКШчЭМ1ЃЌЩшPЕФКсзјБъЮЊtЃЌдђзнзјБъЮЊЉ ![]() t2+t+3ЃЌ
t2+t+3ЃЌ
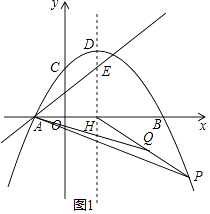
ЁпЕуQЮЊPHЕФжаЕуЃЌ
ЁрSЁїAPQ=SЁїAQHЃЌ
ЁрSЁїAPQ= ![]() SЁїAHPЃЌ
SЁїAHPЃЌ
ЁпSЁїAHP= ![]() AHЃЈ
AHЃЈ ![]() t2ЉtЉ3ЃЉЃЌ
t2ЉtЉ3ЃЉЃЌ
ЁпAH=4ЃЌ
ЁрS= ![]() ЁС4ЁСЃЈЃЈ
ЁС4ЁСЃЈЃЈ ![]() t2ЉtЉ3ЃЉ=
t2ЉtЉ3ЃЉ= ![]() t2ЉtЉ3ЃЈtЃО6ЃЉЃЛ
t2ЉtЉ3ЃЈtЃО6ЃЉЃЛ
ЃЈ3ЃЉНтЃКШчЭМ2ЃЌЙ§PзїxжсЁЂyжсЕФЦНааЯпЗжБ№НЛDHЃЌKQгкMЃЌNЃЌНЛжБЯпDKгкRЃЌ
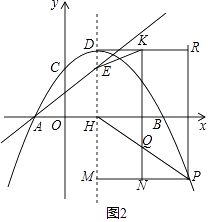
дђЫФБпаЮDKNMЃЌЫФБпаЮKNPRЪЧОиаЮЃЌ
ЩшMN=mЃЌ
ЁрDK=KR=mЃЌ
ЁрPЕуЕФКсзјБъЮЊ2m+2ЃЌДњШыy=Љ ![]() ЃЈxЉ2ЃЉ2+4жаЃЌ
ЃЈxЉ2ЃЉ2+4жаЃЌ
ЕУЕНPЕуЕФзнзјБъЮЊЃКЉm2+4ЃЌЁрDM=RP=m2ЃЌ
ЁрtanЁЯDKE= ![]() =
= ![]() ЃЌ
ЃЌ
ЁрЁЯDKE=ЁЯKPRЃЌ
ЁрEKЁЭPKЃЌ
Ёп2ЁЯDKE+ЁЯHPK=90ЁуЃЌЁЯDKE=ЁЯKPRЃЌЁЯBHP+ЁЯHPK+ЁЯKPR=90ЁуЃЌ
ЁрЁЯDKE=ЁЯPHBЃЌ
ЁрtanЁЯDKE=tanЁЯPHBЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
Ёрm=ЁР ![]() ЃЈm=Љ
ЃЈm=Љ ![]() ЩсШЅЃЉЃЌ
ЩсШЅЃЉЃЌ
Ёрm= ![]() ЃЌ
ЃЌ
ЁрЕуPЕФКсзјБъЮЊ2+2 ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЃЈ1ЃЉЯШЧѓГіEЕФКсзјБъЃЌЕШгкDЕФКсзјБъЃЌМДhжЕЃЌдйАбAзјБъДњШыХзЮяЯпНтЮіЪНЧѓГіk;ЃЈ2ЃЉгЩЁАQЮЊPHЕФжаЕуЁБПЩжЊЁїAPQгыЁїAHPЪЧЭЌИпЕШЕзШ§НЧаЮЃЌУцЛ§ЯрЕШЃЌвђДЫПЩгУtЕФДњЪ§ЪНБэЪОSЁїAHPЃЌдйГЫвд![]() ;(3)гЩ"2ЁЯDKE+ЁЯHPK=90Ёу"ПЩЭЦГіЁЯDKE=ЁЯKPRЃЌЁЯBHP+ЁЯHPK+ЁЯKPR=90ЁуЃЌЁЯDKE=ЁЯKPRЃЌИљОнЖўепЕФе§ЧаЖЈвхЙЙНЈЕШЪНЃЌЧѓГіm.
;(3)гЩ"2ЁЯDKE+ЁЯHPK=90Ёу"ПЩЭЦГіЁЯDKE=ЁЯKPRЃЌЁЯBHP+ЁЯHPK+ЁЯKPR=90ЁуЃЌЁЯDKE=ЁЯKPRЃЌИљОнЖўепЕФе§ЧаЖЈвхЙЙНЈЕШЪНЃЌЧѓГіm.

 жЅТщПЊЛЈПЮГЬаТЬхбщЯЕСаД№АИ
жЅТщПЊЛЈПЮГЬаТЬхбщЯЕСаД№АИ