题目内容
如图，D、E分别是弧
、
的中点，DE交AB、AC于M、M，求证：AM=AN．
【答案】分析：连接OD，OE，根据垂径定理的推论，得到垂直，再根据等角的余角相等证明∠DMB=∠ENC．再结合对顶角相等证明∠AMN=∠ANM，最后根据等角对等边即可证明．
解答：
证明：连接OD、OE分别交AB、AC于点F、G，
∵D、E分别为弧
、
的中点，
∴∠DFM=∠EGN=90°．
∵OD=OE，
∴∠D=∠E．
∵∠D+∠DFM+∠DMB=180°，∠E+∠EGN+∠ENC=180°，
∴∠DMB=∠ENC．
而∠DMB=∠AMN，∠ENC=∠ANM，
∴∠AMN=∠ANM．
∴AM=AN．
点评：此题主要是作辅助线，综合运用了垂径定理以及等腰三角形的判定．
解答：
证明：连接OD、OE分别交AB、AC于点F、G，∵D、E分别为弧
、的中点，∴∠DFM=∠EGN=90°．
∵OD=OE，
∴∠D=∠E．
∵∠D+∠DFM+∠DMB=180°，∠E+∠EGN+∠ENC=180°，
∴∠DMB=∠ENC．
而∠DMB=∠AMN，∠ENC=∠ANM，
∴∠AMN=∠ANM．
∴AM=AN．
点评：此题主要是作辅助线，综合运用了垂径定理以及等腰三角形的判定．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如图，D、E分别是⊙O的半径OA、OB上的点，CD⊥OA，CE⊥OB，CD=CE，则
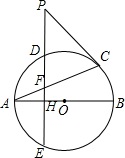如图：AB、AC分别是⊙O的直径和弦，D为弧AC上一点，DE⊥AB于点H，交⊙O于点E，交AC于点F．P为ED延长线上一点，连PC．
如图，D、E分别是弧
如图，D、E分别是弧
、
的中点，DE交AB、AC于M、M，求证：AM=AN．