Question

【题目】在平面直角坐标系中，点是坐标原点，点的坐标是，点的坐标是，点的坐标是，且满足。

（1）请用含的代数式分别表示和；

（2）若，求直线与轴的交点的坐标；

Answer 1

【答案】（1）b=a+2，c=5-a（2）（0,2）

【解析】

（1）根据利用加减消元法即可求出和用含的代数式表示；

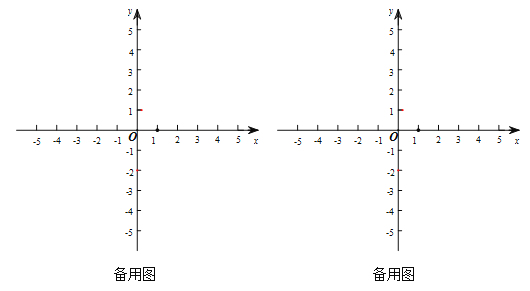
（2）根据题意作出图像，根据得到，由这两个三角形底都为OA,故OA边长上的高相等，故BC∥AO，即可求出a的值，然后求出直线AB的解析式，再求出与y轴的交点即可.

（1）

令②×2得2a-4b-2c=-18③

把①+③得5a-5b=-10，解得b=a+2，

把b=a+2代入①得c=5-a

∴b=a+2，c=5-a

（2）如图，∵

∴，

∵这两个三角形底都为OA,故OA边长上的高相等，

故BC∥AO，

设BC解析式为y=-x+b1，

代入B（1，a+2）得y=-x+a+3,

又直线经过C（5-a,0），代入得a=1,

∴点的坐标是，点的坐标是，点的坐标是，

设直线AB解析式为y=kx+b,代入坐标得，解得

∴直线AB的解析式为y=x+2,

∴直线与轴的交点的坐标为（0,2）