Question

【题目】如图，的点，在上，与相交于点，连接，，，．

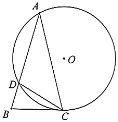
（1）求圆心到弦的距离；

（2）若．

①求证：是的切线；

②求的长．

Answer 1

【答案】（1）圆心到的距离为；（2）①见解析；②．

【解析】

（1）连接OD，OC，过O作OE⊥DC于E，得到△OCD是等边三角形，求得OD＝OC＝CD＝，解直角三角形即可得到结论；

（2）①由（1）得，△ODC是等边三角形，求得∠OCD＝60°，证明，根据相似三角形的性质得到∠A＝∠BCD＝30°，求得∠OCB＝90°，于是得到BC是⊙O的切线；

②根据相似三角形的性质得到CB2＝ABDB，过D作DF⊥AC于F，得到∠AFD＝∠CFD＝90°，解直角三角形求出AD，再证明，即可解决问题．

解：（1）连接，，过点作于点，

∵内接于，，

∴，

∵，，

∴为等边三角形，

∴，

∵，

∴，，，

∴，即圆心到的距离为；

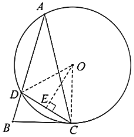
（2）①由（1）得为等边三角形，

∴,

∵，，

∴，

∵，

∴，

∴，

∴，

∴是的切线；

②∵，

∴，即，

过点作于点，

∴，

∵，，，

∴，，

∵，，

∴，

∴，

设为，则，

解得：，

∴（），

∴．