Question

已知点M（3，2），N（1，-1），点P在y轴上，求使得△PMN的周长最小的点P的坐标及△PMN周长的最小值．

Answer 1

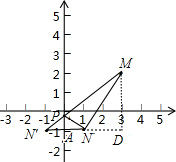解：作出N点关于y轴的对称点N′点，连接N′M，与y轴交点即是P点，延长N′N，作MD⊥N′N，垂足为D，
∵点M（3，2），N（1，-1），
∴MD=3，DN′=4，
易得△N′PA∽△N′MD，
∴，
∴，
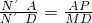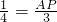解得：AP=，
∴OP=，
∴使得△PMN的周长最小的点P的坐标为：（0，-）；
∴S_△PNM=S_△MNN′-S_△PNN′=DM×NN′-NN′×AP=×2×（3-）=，
∴△PMN周长的最小值为：．
分析：首先利用轴对称求出P点的坐标，再利用三角形相似求出OP的长，即可得出P点的坐标，再利用三角形面积求法即可得出最小面积．
点评：此题主要考查了轴对称中最短路径求法以及坐标与图形性质，求出P点坐标是解决问题的关键．