题目内容
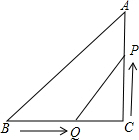 如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△CBA相似?
如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△CBA相似?
解:设经过x秒后,两三角形相似,则CQ=(8-2x)cm,CP=xcm,
∵∠C=∠C=90°,
∴当 或
或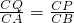 时,两三角形相似.
时,两三角形相似.
(1)当 时,
时,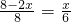 ,∴x=
,∴x= ;
;
(2)当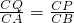 时,
时,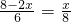 ,∴x=
,∴x=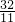 .
.
所以,经过 秒或
秒或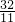 秒后,两三角形相似.
秒后,两三角形相似.
分析:此题要根据相似三角形的性质设出未知数,即经过x秒后,两三角形相似,然后根据速度公式求出他们移动的长度,再根据相似三角形的性质列出分式方程求解.
点评:本题综合考查了路程问题,相似三角形的性质及一元一次方程的解法.
∵∠C=∠C=90°,
∴当
 或
或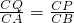 时,两三角形相似.
时,两三角形相似.(1)当
 时,
时,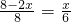 ,∴x=
,∴x= ;
;(2)当
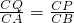 时,
时,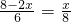 ,∴x=
,∴x=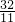 .
.所以,经过
 秒或
秒或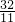 秒后,两三角形相似.
秒后,两三角形相似.分析:此题要根据相似三角形的性质设出未知数,即经过x秒后,两三角形相似,然后根据速度公式求出他们移动的长度,再根据相似三角形的性质列出分式方程求解.
点评:本题综合考查了路程问题,相似三角形的性质及一元一次方程的解法.

练习册系列答案
相关题目

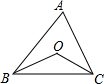 如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为
如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为 如图在△ABC中,∠A=45°,tanB=3,BC=
如图在△ABC中,∠A=45°,tanB=3,BC= 已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,
已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE, 如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是
如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是