Question

如图，直线AE与以AB为直径的⊙O相切于点A，点C、D在⊙O上，并分别位于AB的两侧，∠EAC＝60°．

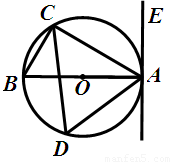
⑴ 求∠D的度数；

⑵ 当BC＝4时，求劣弧AC的长．

 

Answer 1

【答案】

（1）60°（2）

【解析】

试题分析：解：⑴ ∵AE是⊙O的切线，

∴BA⊥AE，即∠BAE=90°．

∵∠EAC＝60°，∴∠BAC=30°．

∵AB是⊙O的直径，∴∠ACB=90°．

∴∠B=∠ACB－∠BAC=60°．

∵∠B与∠D都是弧AC所对的圆周角，

∴∠D =∠B =60°．

⑵ 联结OC，

∵OB=OC，∠B=60°，∴△OBC是等边三角形．

∴OB=BC=4，∠BOC=60°．

∴∠AOC=120°．

∴劣弧AC的长＝＝．

考点：圆的切线性质，圆周角，弧长公式

点评：难度中等，掌握圆的切线和圆周角的性质，利用弧长公式可以解出此题。