题目内容
如图,△ABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE.若∠A=30°,AB=AC,则∠BDE的度数为( ).

A.45° B.52.5°
C.67.5° D.75°
【答案】
C.
【解析】
试题分析:根据AB=AC,利用三角形内角和定理求出∠ABC的度数,再利用等腰三角形的性质和三角形内角和定理求出∠DBC=30°,然后即可求出∠BDE的度数:
∵AB=AC,∴∠ABC=∠ACB.
∵∠A=30°,∴∠ABC=∠ACB= .
.
∵以B为圆心,BC长为半径画弧,∴BE=BD=BC。∴∠BDC=∠ACB=75°.
∴∠CBD .∴∠DBE=75°
.∴∠DBE=75° 30°=45°.
30°=45°.
∴∠BED=∠BDE= .
.
故选C.
考点: 1.等腰三角形的性质;2.三角形内角和定理.

练习册系列答案
相关题目
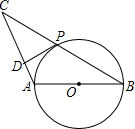 已知:如图,△ABC中,以AB为直径的⊙O交BC于点P,且P为BC中点,PD⊥AC于点D.
已知:如图,△ABC中,以AB为直径的⊙O交BC于点P,且P为BC中点,PD⊥AC于点D. (2013•高淳县二模)如图,△ABC中,以AB为直径的⊙O交AC于D,交BC于E,已知CD=AD.
(2013•高淳县二模)如图,△ABC中,以AB为直径的⊙O交AC于D,交BC于E,已知CD=AD. 如图,△ABC中,以B为圆心,BC长为半径的⊙B交边AB于D,AE⊥AB交CD的延长线于E,并且AE=AC.
如图,△ABC中,以B为圆心,BC长为半径的⊙B交边AB于D,AE⊥AB交CD的延长线于E,并且AE=AC. (2007•攀枝花)如图,△ABC中,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N,且BA•BM=BC•BN.
(2007•攀枝花)如图,△ABC中,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N,且BA•BM=BC•BN. 如图,△ABC中,以BC为边向外作△BCD,把△ABD绕着点D按顺时针方向旋转60°得到△ECD的位置,A、C、E三点恰好在同一直线上.
如图,△ABC中,以BC为边向外作△BCD,把△ABD绕着点D按顺时针方向旋转60°得到△ECD的位置,A、C、E三点恰好在同一直线上.