题目内容
 如图,将边长为6的正方形ABCD折叠,使点D落在BC边上的E点处,点A落在点F处,折痕为MN,测得∠MEC=30°,则线段BE的长为________.
如图,将边长为6的正方形ABCD折叠,使点D落在BC边上的E点处,点A落在点F处,折痕为MN,测得∠MEC=30°,则线段BE的长为________.
6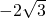
分析:由四边形ABCD是正方形,即可得∠C=90°,CD=BC=6,又由∠MEC=30°,根据直角三角形中,30°角所对的直角边等于斜边的一半,即可求得CM与EM的长,然后由勾股定理求得EC的长,继而求得线段BE的长.
解答:∵四边形ABCD是正方形,
∴∠C=90°,CD=BC=6,
∵∠MEC=30°,
∴在Rt△MEC中,EM=2CM,
由折叠的性质可得:DM=EM,
∵DM+CM=CD=6,
即3CM=6,
解得:CM=2,EM=4,
在Rt△MEC中,EC= =2
=2 ,
,
∴BE=BC-EC=6-2 .
.
故答案为:6-2 .
.
点评:此题考查了折叠的性质、正方形的性质、勾股定理以及含30°角的直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.
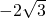
分析:由四边形ABCD是正方形,即可得∠C=90°,CD=BC=6,又由∠MEC=30°,根据直角三角形中,30°角所对的直角边等于斜边的一半,即可求得CM与EM的长,然后由勾股定理求得EC的长,继而求得线段BE的长.
解答:∵四边形ABCD是正方形,
∴∠C=90°,CD=BC=6,
∵∠MEC=30°,
∴在Rt△MEC中,EM=2CM,
由折叠的性质可得:DM=EM,
∵DM+CM=CD=6,
即3CM=6,
解得:CM=2,EM=4,
在Rt△MEC中,EC=
 =2
=2 ,
,∴BE=BC-EC=6-2
 .
.故答案为:6-2
 .
.点评:此题考查了折叠的性质、正方形的性质、勾股定理以及含30°角的直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
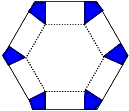 如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为 (2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为
(2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为