题目内容
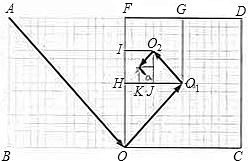
如图,是由两个正方形组成的长方形花坛ABCD,小明从顶点A沿着花坛间小路走到长边中点O,再从中点O走到正方形OCDF的中心O1,再从中心O1走到正方形O1GFH的中心O2,又从中心O2走到正方形O2IHJ的中心O3,再 从O3走到正方形O3KJP的中心O4,一共走了31
从O3走到正方形O3KJP的中心O4,一共走了31 m,则长方形花坛ABCD的周长是
m,则长方形花坛ABCD的周长是
- A.36m
- B.48m
- C.96m
- D.60m
C
分析:用正方形O3KJP的边长将O3O4,O2O3,O1O2,OO1的长表示出来,相加等于所走的路程,将正方形O3KJP的边长求出,根据各个正方形之间的关系,进而可将正方形ABCD的周长求出.
解答: 解:设正方形O3KJP的边长为a,根据正方形的性质知:O3O4=
解:设正方形O3KJP的边长为a,根据正方形的性质知:O3O4=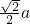
正方形O2IHJ的边长为2a,O2O3= a,
a,
正方形O1GFH的边长为4a,O1O2= a,
a,
正方形OCDF的边长为8a,OO1= a,
a,
∵AO=2OO1=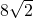 am,
am,
∴ a+
a+ a+
a+ a+
a+ a+
a+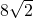 a=
a= ,
,
解得:a=2m,
∴FD=8a=16m,
∴长方形花坛ABCD的周长是2×(2FD+CD)=6FD=96m.
故选C.
点评:解答本题要充分利用正方形的特殊性质.
分析:用正方形O3KJP的边长将O3O4,O2O3,O1O2,OO1的长表示出来,相加等于所走的路程,将正方形O3KJP的边长求出,根据各个正方形之间的关系,进而可将正方形ABCD的周长求出.
解答:
 解:设正方形O3KJP的边长为a,根据正方形的性质知:O3O4=
解:设正方形O3KJP的边长为a,根据正方形的性质知:O3O4=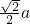
正方形O2IHJ的边长为2a,O2O3=
 a,
a,正方形O1GFH的边长为4a,O1O2=
 a,
a,正方形OCDF的边长为8a,OO1=
 a,
a,∵AO=2OO1=
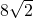 am,
am,∴
 a+
a+ a+
a+ a+
a+ a+
a+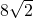 a=
a= ,
,解得:a=2m,
∴FD=8a=16m,
∴长方形花坛ABCD的周长是2×(2FD+CD)=6FD=96m.
故选C.
点评:解答本题要充分利用正方形的特殊性质.

练习册系列答案
相关题目
 从O3走到正方形O3KJP的中心O4,一共走了31
从O3走到正方形O3KJP的中心O4,一共走了31
 m,则长方形花坛ABCD的周长是( )
m,则长方形花坛ABCD的周长是( )
 m,则长方形花坛ABCD的周长是( )
m,则长方形花坛ABCD的周长是( )
