题目内容
5.已知p2-2p-5=0,5q2+2q-1=0,其中p、q为实数,求p2+$\frac{1}{{q}^{2}}$的值.分析 将5q2+2q-1=0变形为($\frac{1}{q}$)2-2•$\frac{1}{q}$-5=0,结合p2-2p-5=0即可得出p和$\frac{1}{q}$为方程x2-2x-5=0的两个实数根,根据根与系数的关系即可得出p+$\frac{1}{q}$=2、p•$\frac{1}{q}$=-5,再将其代入p2+$\frac{1}{{q}^{2}}$=$(p+\frac{1}{q})^{2}$-2p•$\frac{1}{q}$中即可得出结论.
解答 解:∵5q2+2q-1=0,
∴q≠0,($\frac{1}{q}$)2-2•$\frac{1}{q}$-5=0,
又∵p2-2p-5=0,
∴p和$\frac{1}{q}$为方程x2-2x-5=0的两个实数根,
∴p+$\frac{1}{q}$=2,p•$\frac{1}{q}$=-5,
∴p2+$\frac{1}{{q}^{2}}$=$(p+\frac{1}{q})^{2}$-2p•$\frac{1}{q}$=22-2×(-5)=14.
点评 本题主要考查一元二次方程根与系数的关系,熟练掌握根与系数关系的公式是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
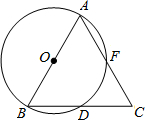 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F. 如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,EF交AD于点O,求证:OF=OE.
如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,EF交AD于点O,求证:OF=OE.