题目内容
(2011•利川市一模)观察下列各式的特征:
×2=
+2;
×3=
+3;
×4=
+4;….试用正整数n的等式表示以上各式反映的规律:
×(n+1)=
+(n+1)(n为正整数)
×(n+1)=
+(n+1)(n为正整数).
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
| n+1 |
| n |
| n+1 |
| n |
| n+1 |
| n |
| n+1 |
| n |
分析:由于
×2=
+2,
×3=
+3,
×4=
+4,得到一个假分数(分子比分母大1)与分子相同的数的积等于它们的和,用含n的式子表示为
×(n+1)=
+(n+1)(n为正整数).
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
| n+1 |
| n |
| n+1 |
| n |
解答:解:∵
×2=
+2,
×3=
+3,
×4=
+4,
…
∴
×(n+1)=
+(n+1)(n为正整数).
故答案为:
×(n+1)=
+(n+1)(n为正整数).
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
…
∴
| n+1 |
| n |
| n+1 |
| n |
故答案为:
| n+1 |
| n |
| n+1 |
| n |
点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
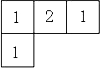 (2011•利川市一模)如图所示,是几个相同小正方体所搭成几何体的俯视图,小正方形内的数字表示在该位置的小正方体的个数.则这个几何体的主视图是( )
(2011•利川市一模)如图所示,是几个相同小正方体所搭成几何体的俯视图,小正方形内的数字表示在该位置的小正方体的个数.则这个几何体的主视图是( ) (2011•利川市一模)如图,反映的是九(3)班学生某次数学考试成绩不及格、及格、优分的人数分布直方图和扇形统计图(部分),则下列说法中不正确的是( )
(2011•利川市一模)如图,反映的是九(3)班学生某次数学考试成绩不及格、及格、优分的人数分布直方图和扇形统计图(部分),则下列说法中不正确的是( )