题目内容
如图，直线y=-2x+4与x轴，y轴分别相交于A，B两点，C为OB上一点，且∠1=∠2，则S△ABC=（ ）
A．1
B．2
C．3
D．4
【答案】分析：本题可先根据直线的方程求出A、B两点的坐标，再根据角相等可得出三角形相似，最后通过相似比即可得出S△ABC的大小．
解答：解：∵直线y=-2x+4与x轴，y轴分别相交于A，B两点
∴OA=2，OB=4
又∵∠1=∠2
∴∠BAO=∠OCA
∴△OAC∽△OAB
则OC：OA=OA：OB=1：2
∴OC=1，BC=3，
∴S△ABC=
×2×3=3
故选C．
点评：主要考查了一次函数图象上点的特征和点的坐标的意义以及与相似三角形相结合的具体运用．要把点的坐标有机地和图形结合起来求解．
解答：解：∵直线y=-2x+4与x轴，y轴分别相交于A，B两点
∴OA=2，OB=4
又∵∠1=∠2
∴∠BAO=∠OCA
∴△OAC∽△OAB
则OC：OA=OA：OB=1：2
∴OC=1，BC=3，
∴S△ABC=
×2×3=3故选C．
点评：主要考查了一次函数图象上点的特征和点的坐标的意义以及与相似三角形相结合的具体运用．要把点的坐标有机地和图形结合起来求解．
练习册系列答案
星级口算天天练系列答案
相关题目
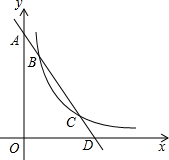如图，直线y=-2x+b与y轴交于点A，与x轴交于点D，与双曲线
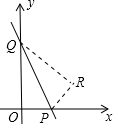如图，直线y=-2x+6与x轴、y轴分别交于P、Q两点，把△POQ沿PQ翻折，点O落在R处，则点R的坐标是
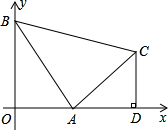腰直角△ABC，∠BAC=90°，过C作CD⊥x轴，垂足为D．
轴分别交于点C、D．直线EB交x轴于点F．
如图，直线y=-2x+8与两坐标轴分别交于P，Q两点，在线段PQ上有一点A，过点A分别作两坐标轴的垂线，垂足分别为B、C．