题目内容
 如图,直角坐标系中,正方形CDEF的边长为4,且CD∥y轴,直线y=-
如图,直角坐标系中,正方形CDEF的边长为4,且CD∥y轴,直线y=- x-1过点C,且交x轴,y轴于点A、B,若点P沿正方形ABCD运动一周,则以P为圆心、
x-1过点C,且交x轴,y轴于点A、B,若点P沿正方形ABCD运动一周,则以P为圆心、 为半径的圆动与直线GB相切的次数为
为半径的圆动与直线GB相切的次数为
- A.一次
- B.两次
- C.三次
- D.四次
B
分析:如图,作PH⊥BC于H,GM⊥BC与M,根据条件利用勾股定理就可以求出PD、GC的值,就可以求出⊙P的运动位置,从而确定⊙P与直线CB的相切次数.
解答:如图,作PH⊥BC于H,GM⊥BC与M,PN⊥CF,
∴∠PHS=∠GMC=∠PNC=90°.
∵四边形CDEF是正方形,
∴∠E=∠F=∠FCD=∠D=90°,CD=DE=EF=CF=4.CD∥y轴,
∴∠HPN=∠MGC=∠BAO,
∵直线y=- x-1,当y=0时,x=-2,
x-1,当y=0时,x=-2,
当x=0时,y=-1,
∴A(-2,0),B(0,-1),
∴OA=2,OB=1,
∴tan∠OAB= ,
,
∴tan∠HPN=tan∠MGC= .
.
当PH= 时,HS=
时,HS= ,
,
在Rt△PHS中,由勾股定理得:
PS= ,
,
∴SN= ,
,
∴NC=3,
∴PD=3,
∴P点运动到离D点的距离为3时,⊙P与直线相切,
当P点运动到G点,GM= 时,则MA=
时,则MA= ,
,
在Rt△GMC中,由勾股定理,得
GC= ,
,
∴DG= ,
,
∴P点运动到离G点的距离为 时,⊙P与直线相切,
时,⊙P与直线相切,
∴⊙P与直线CB相切2次.
故选B.
点评:本题考查了一次函数的解析式的运用,三角函数值的运用,勾股定理的运用,相切的判定及性质的运用,解答时灵活运用三角函数值根据勾股定理求解是关键.
分析:如图,作PH⊥BC于H,GM⊥BC与M,根据条件利用勾股定理就可以求出PD、GC的值,就可以求出⊙P的运动位置,从而确定⊙P与直线CB的相切次数.
解答:如图,作PH⊥BC于H,GM⊥BC与M,PN⊥CF,
∴∠PHS=∠GMC=∠PNC=90°.
∵四边形CDEF是正方形,
∴∠E=∠F=∠FCD=∠D=90°,CD=DE=EF=CF=4.CD∥y轴,
∴∠HPN=∠MGC=∠BAO,
∵直线y=-
 x-1,当y=0时,x=-2,
x-1,当y=0时,x=-2,当x=0时,y=-1,
∴A(-2,0),B(0,-1),
∴OA=2,OB=1,
∴tan∠OAB=
 ,
,∴tan∠HPN=tan∠MGC=
 .
.当PH=
 时,HS=
时,HS= ,
,在Rt△PHS中,由勾股定理得:
PS=
 ,
,∴SN=
 ,
,∴NC=3,
∴PD=3,

∴P点运动到离D点的距离为3时,⊙P与直线相切,
当P点运动到G点,GM=
 时,则MA=
时,则MA= ,
,在Rt△GMC中,由勾股定理,得
GC=
 ,
,∴DG=
 ,
,∴P点运动到离G点的距离为
 时,⊙P与直线相切,
时,⊙P与直线相切,∴⊙P与直线CB相切2次.
故选B.
点评:本题考查了一次函数的解析式的运用,三角函数值的运用,勾股定理的运用,相切的判定及性质的运用,解答时灵活运用三角函数值根据勾股定理求解是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
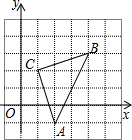 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为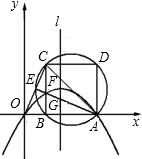 ?若存在,请求出所有这样的点;若不存在,请说明理由.
?若存在,请求出所有这样的点;若不存在,请说明理由. 在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4),
在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4), 如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是
如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是 在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示:
在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示: