题目内容
一个扇形的周长是4,则这个扇形的面积最大值是________.
1
分析:由扇形的周长和面积公式都和半径和弧长有关,故可设出半径和弧长,表示出周长和面积公式,寻找关系即可.
解答:设半径为r,弧长为l,则周长为2r+l=4,面积为S= lr,
lr,
∵4=2r+l≥2 (当且仅当r=l时取“=”),
(当且仅当r=l时取“=”),
∴rl≤2,
∴S= lr≤
lr≤ ×2=1,
×2=1,
∴S的最大值是1.
故答案是:1.
点评:本题考查扇形的周长和面积公式及利用基本不等式求最值,考查运用所学知识解决问题的能力.
分析:由扇形的周长和面积公式都和半径和弧长有关,故可设出半径和弧长,表示出周长和面积公式,寻找关系即可.
解答:设半径为r,弧长为l,则周长为2r+l=4,面积为S=
 lr,
lr,∵4=2r+l≥2
 (当且仅当r=l时取“=”),
(当且仅当r=l时取“=”),∴rl≤2,
∴S=
 lr≤
lr≤ ×2=1,
×2=1,∴S的最大值是1.
故答案是:1.
点评:本题考查扇形的周长和面积公式及利用基本不等式求最值,考查运用所学知识解决问题的能力.

练习册系列答案
相关题目

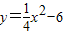 与直线
与直线 相交于A,B两点.
相交于A,B两点. 是否成立;
是否成立; .
.
 与直线
与直线 相交于A,B两点.
相交于A,B两点. 是否成立;
是否成立; .
.