题目内容
已知抛物线y=x2+kx- k2(k为常数,且k>0).
k2(k为常数,且k>0).
(1)证明:此抛物线与x轴总有两个交点;
(2)设抛物线与x轴交于M、N两点,若这两点到原点的距离分别为OM、ON,且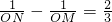 ,求k的值.
,求k的值.
解:(1)△=k2-4×1×(- k2)=4k2
k2)=4k2
∵k>0,
∴△=4k2>0.
∴此抛物线与x轴总有两个交点.
(2)方程x2+kx- k2=0的解是:
k2=0的解是:
x= k或x=-
k或x=- k.
k.
∵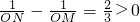 ,
,
∴OM>ON.
∵k>0,
∴M(- k,0),N(
k,0),N( k,0),
k,0),
∴OM= k,ON=
k,ON= k.
k.
∴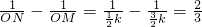 ,
,
解得k=2.
分析:(1)可让y=0,然后证所得的一元二次方程满足△>0即可.
(2)根据(1)的一元二次方程可求出方程的两个根,也就是M、N两点的横坐标,根据给出的条件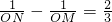 ,可得出M点横坐标的绝对值要大于N的横坐标的绝对值,因此可据此确定M、N两点的坐标,即可得出OM,ON的长,然后代入给出的等量关系中,即可求出k的值.
,可得出M点横坐标的绝对值要大于N的横坐标的绝对值,因此可据此确定M、N两点的坐标,即可得出OM,ON的长,然后代入给出的等量关系中,即可求出k的值.
点评:本题考查的是二次函数与一元二次方程的关系,当二次函数的y值为0时就可转化成一元二次方程.
 k2)=4k2
k2)=4k2∵k>0,
∴△=4k2>0.
∴此抛物线与x轴总有两个交点.
(2)方程x2+kx-
 k2=0的解是:
k2=0的解是:x=
 k或x=-
k或x=- k.
k.∵
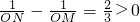 ,
,∴OM>ON.
∵k>0,
∴M(-
 k,0),N(
k,0),N( k,0),
k,0),∴OM=
 k,ON=
k,ON= k.
k.∴
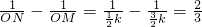 ,
,解得k=2.
分析:(1)可让y=0,然后证所得的一元二次方程满足△>0即可.
(2)根据(1)的一元二次方程可求出方程的两个根,也就是M、N两点的横坐标,根据给出的条件
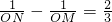 ,可得出M点横坐标的绝对值要大于N的横坐标的绝对值,因此可据此确定M、N两点的坐标,即可得出OM,ON的长,然后代入给出的等量关系中,即可求出k的值.
,可得出M点横坐标的绝对值要大于N的横坐标的绝对值,因此可据此确定M、N两点的坐标,即可得出OM,ON的长,然后代入给出的等量关系中,即可求出k的值.点评:本题考查的是二次函数与一元二次方程的关系,当二次函数的y值为0时就可转化成一元二次方程.

练习册系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.