题目内容
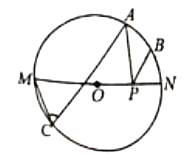
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() ,
,![]() 是
是![]() 上的三点,
上的三点,![]() ,
,![]() 点是
点是![]() 的中点,
的中点,![]() 点是
点是![]() 上一动点,若
上一动点,若![]() 的半径为1,则
的半径为1,则![]() 的最小值为( )
的最小值为( )
A.1B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
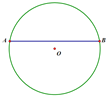
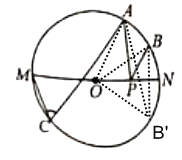
作点B关于MN的对称点B′,连接OA、OB、OB′、AB′,根据轴对称确定最短路线问题可得PA+PB的最小值=AB′,根据在同圆或等圆中,同弧所对的圆心角等于圆周角的2倍求出∠AOM=120°,然后可得∠AON=60°,再求出∠BON=30°,根据对称性可得∠B′ON=∠BON=30°,然后易得∠AOB′=90°,从而判断出△AOB′是等腰直角三角形,再根据等腰直角三角形的性质可得AB′的长度.
解:作点B关于MN的对称点B′,连接OA、OB、OB′、AB′,则PA+PB的最小值=AB′,
∵∠ACM=60°,
∴∠AOM=120°,
∴∠AON=180°-∠AOM=60°,
∵点B为![]() 的中点,
的中点,
∴∠BON=![]() ∠AON=
∠AON=![]() ×60°=30°,
×60°=30°,
由对称性可得,∠B′ON=∠BON=30°,
∴∠AOB′=∠AON+∠B′ON=60°+30°=90°,
∴△AOB′是等腰直角三角形,
∴AB′=![]() OA=
OA=![]() ,即PA+PB的最小值为
,即PA+PB的最小值为![]() .
.
故选:C.

练习册系列答案
相关题目