题目内容
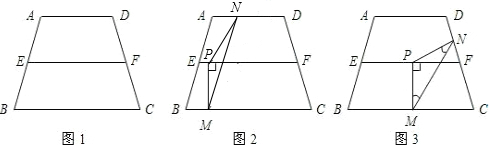
①如图1,在等腰梯形ABCD中,AD∥BC,AB=AD=CD.若∠ABC=60°,BC=12,则梯形ABCD的周长为________.
②如图2,在梯形ABCD中,AB∥DC,DB⊥AD,AD=DC=BC=2cm,那么梯形ABCD的面积是________.
③如图3,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.则∠ABD的度数为________;若AD=2,则对角线BD的长为________.

30 3 cm2 90° 2
cm2 90° 2
分析:①过D作DE∥AB交BC于E,得出平行四边形和等边三角形,推出AD=BE,DE=DC=EC,求出AD,即可求出答案;
②过D作DF⊥AB于F,求出∠DBA=30°,求出AB和高DF,即可求出梯形面积;
③求出∠A=∠ABC,求出∠DBA=30°,即可求出∠ADB=90°,根据AD求出AB,根据勾股定理求出BD即可.
解答:①过D作DE∥AB交BC于E,
∵DE∥AB,AD∥BC,
∴四边形ABED是平行四边形,
∴AB=DE,AD=BE,
∵四边形ABCD是等腰梯形,
∴∠B=∠C=60°,AB=DC=DE,
∴△DEC是等边三角形,
∴EC=DE=DC,
∵AB=AD=CD,BC=12,AD=BE,EC=DC,
∴BE=EC=6,
∴AD=6=AB=DC,
∴梯形ABCD的周长是AD+DC+BC+AB=6+6+12+6=30,
故答案为:30.
②∵四边形ABCD是等腰梯形,
∴∠A=∠CBA,
∵DC∥AB,
∴∠CDB=∠DBA,
∵DC=CB,
∴∠CDB=∠CBD,
∴∠CBD=∠DBA= ABC=
ABC= ∠A,
∠A,
∵BD⊥AD,
∴∠ADB=90°,
∴∠A+∠DBA=90°,
∴∠A=60°,∠DBA=30°,
∴AB=2AD=4cm,
过D作DF⊥AB于F,
∵∠A=60°,
∴∠ADF=30°,
∴AF= AD=1cm,
AD=1cm,
由勾股定理得:DF= =
= (cm),
(cm),
∴梯形ABCD的面积是 ×(CD+AB)×DF=
×(CD+AB)×DF= ×(2+4)×
×(2+4)× =3
=3 (cm2)
(cm2)
故答案为:3 cm2.
cm2.
③∵BD平分∠CBA,
∴∠CBD=∠ABD,
∵四边形ABCD是等腰梯形,∠A=60°,
∴∠A=∠ABC=60°,
∴∠DBA=30°,
∴∠ADB=180°-60°-30°=90°,
∵∠ADB=90°,∠DBA=30°,AD=2,
∴AB=2AD=4,由勾股定理得:BD= =2
=2 ,
,
故答案为:90°,2 .
.
点评:本题综合考查了等腰梯形性质,平行四边形的性质和判定,含30度角的直角三角形性质,勾股定理,三角形的内角和定理等知识点的运用.
 cm2 90° 2
cm2 90° 2
分析:①过D作DE∥AB交BC于E,得出平行四边形和等边三角形,推出AD=BE,DE=DC=EC,求出AD,即可求出答案;
②过D作DF⊥AB于F,求出∠DBA=30°,求出AB和高DF,即可求出梯形面积;
③求出∠A=∠ABC,求出∠DBA=30°,即可求出∠ADB=90°,根据AD求出AB,根据勾股定理求出BD即可.
解答:①过D作DE∥AB交BC于E,
∵DE∥AB,AD∥BC,
∴四边形ABED是平行四边形,
∴AB=DE,AD=BE,
∵四边形ABCD是等腰梯形,
∴∠B=∠C=60°,AB=DC=DE,
∴△DEC是等边三角形,
∴EC=DE=DC,
∵AB=AD=CD,BC=12,AD=BE,EC=DC,
∴BE=EC=6,
∴AD=6=AB=DC,
∴梯形ABCD的周长是AD+DC+BC+AB=6+6+12+6=30,
故答案为:30.
②∵四边形ABCD是等腰梯形,

∴∠A=∠CBA,
∵DC∥AB,
∴∠CDB=∠DBA,
∵DC=CB,
∴∠CDB=∠CBD,
∴∠CBD=∠DBA=
 ABC=
ABC= ∠A,
∠A,∵BD⊥AD,
∴∠ADB=90°,
∴∠A+∠DBA=90°,
∴∠A=60°,∠DBA=30°,
∴AB=2AD=4cm,
过D作DF⊥AB于F,
∵∠A=60°,
∴∠ADF=30°,
∴AF=
 AD=1cm,
AD=1cm,由勾股定理得:DF=
 =
= (cm),
(cm),∴梯形ABCD的面积是
 ×(CD+AB)×DF=
×(CD+AB)×DF= ×(2+4)×
×(2+4)× =3
=3 (cm2)
(cm2)故答案为:3
 cm2.
cm2.③∵BD平分∠CBA,
∴∠CBD=∠ABD,
∵四边形ABCD是等腰梯形,∠A=60°,
∴∠A=∠ABC=60°,
∴∠DBA=30°,
∴∠ADB=180°-60°-30°=90°,
∵∠ADB=90°,∠DBA=30°,AD=2,
∴AB=2AD=4,由勾股定理得:BD=
 =2
=2 ,
,故答案为:90°,2
 .
.点评:本题综合考查了等腰梯形性质,平行四边形的性质和判定,含30度角的直角三角形性质,勾股定理,三角形的内角和定理等知识点的运用.

练习册系列答案
相关题目
 条件时,其一定平分梯形的面积?(只要求说出条件,不需证明)
条件时,其一定平分梯形的面积?(只要求说出条件,不需证明)
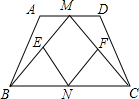 (2009•黔南州)杨老师在上四边形时给学生出了这样一个题.如图,若在等腰梯形ABCD中,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点时.提出以下问题:
(2009•黔南州)杨老师在上四边形时给学生出了这样一个题.如图,若在等腰梯形ABCD中,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点时.提出以下问题: