题目内容
如图1,在直角坐标系中,点A在y轴的正半轴上,点B为x轴正半轴上一点,点D的坐标为(-
,1),△AOD和△BDC(点B、D、C沿顺时针方向排列)都为等边三角形.
(1)求证:△BOD≌△CAD;
(2)若△BDC的边长为7,求AC的长及点C的坐标;
(3)设(2)中点B的位置为初始位置,点B在x轴上由初始位置以1个单位/秒的速度向左运动,等边△BCD的大小也随之变化,在运动过程中△AOC是否能成为等腰三角形?如果能,请直接写出运动时间t的值;如果不能,请说明理由.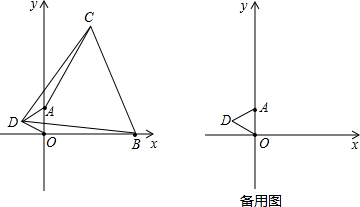
| 3 |
(1)求证:△BOD≌△CAD;
(2)若△BDC的边长为7,求AC的长及点C的坐标;
(3)设(2)中点B的位置为初始位置,点B在x轴上由初始位置以1个单位/秒的速度向左运动,等边△BCD的大小也随之变化,在运动过程中△AOC是否能成为等腰三角形?如果能,请直接写出运动时间t的值;如果不能,请说明理由.

分析:(1)由条件可以求出DC=DB,DA=DO,∠CDA=∠ODB,从而可以求出△BOD≌△CAD,
(2)作DE⊥x轴于点E,由点D的坐标可以求出DE、OE的值,在Rt△DEB中由勾股定理可以求出BE的值进而求出OB的值,可以代换出AC的值,设出C点的坐标,利用两点间的距离公式建立方程组就可以求出点C的坐标.
(3)点B在运动的过程中就会有AC=AO,OC=AC,OA=OC的不同情况下△AOC为等腰三角形,根据AC=OB的条件就可以求出其对应的t值.
(2)作DE⊥x轴于点E,由点D的坐标可以求出DE、OE的值,在Rt△DEB中由勾股定理可以求出BE的值进而求出OB的值,可以代换出AC的值,设出C点的坐标,利用两点间的距离公式建立方程组就可以求出点C的坐标.
(3)点B在运动的过程中就会有AC=AO,OC=AC,OA=OC的不同情况下△AOC为等腰三角形,根据AC=OB的条件就可以求出其对应的t值.
解答:解:(1)∵△AOD和△BDC是等边三角形,
∴DC=DB,DA=DO,∠CDB=∠ODA=60°,
∴∠CDB-∠ADO=∠ODA-∠ADO,
∴∠CDA=∠ODB,
∴△BOD≌△CAD;
(2)作DE⊥x轴于点E,
∵△BOD≌△CAD,
∴OB=AC,
∵点D的坐标为(-
,1),
∴DE=1,OE=
,
∴在Rt△BDE中,BD=CD=BC=7,由勾股定理,得
BE=4
,
∴OB=3
∴AC=3
.B(3
,0)
如图,设点C(x,y),在Rt△DHC和Rt△CGB中,由勾股定理,得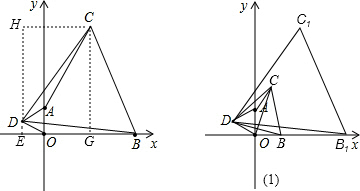
,解得
或
(不符合题意)
∴C(
,
).
(3)如图(1)当OA=AC时,△AOC是等腰三角形,
∵OB=AC,
∴OA=OB=2,
∴t=3
-2.
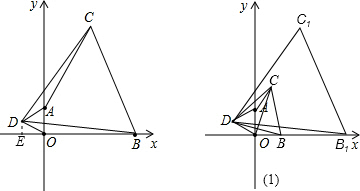
如图(2),当B运动到B′时,C点落在OA的垂直平分线上C′时,△AOC是等腰三角形,△DB′C′是等边三角形,连接OC′,
∴四边形DB′OC′是菱形,
∴B′D=B′O=OC′,OE=1,C′E=
,
∴OC′=
,
∴t=
+3
=
如图(2)当B运动到B″时,B″O=DO,这时AO=AC″,△AOC是等腰三角形,
∴OB″=2,
∴t=OB″+OB=3
+2,
如图(2)当B运动到B3时,点C3在AO的中垂线上时,△AOC3是等腰三角形,
∴△B3DO是Rt△,且∠DB3O=60°,∠B3OD=30°,
∴∠B3DO=90°,且OD=2,由勾股定理,得
∴OB3=
,
∴t=3
+
=
,
∵点B、D、C要沿顺时针方向排列,
∴t值不存在.
当B运动到B5时,DB5=DO=2,C点在第三象限,即C5.
∴∠DB5O=∠B5OD=30°.
∵△B5C5D是等边三角形,
∴∠B5DC5=60°,
∴DC5⊥OB5.
∴由勾股定理可以求出
OB5=
,
∴OB5=2
,∴t=2
+3
=5
综上所述:∴t1=3
-2,t2=
,t3=3
+2,t4=5
.
⑤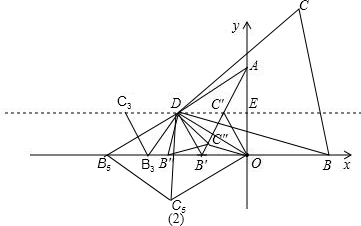
∴DC=DB,DA=DO,∠CDB=∠ODA=60°,
∴∠CDB-∠ADO=∠ODA-∠ADO,
∴∠CDA=∠ODB,
∴△BOD≌△CAD;
(2)作DE⊥x轴于点E,
∵△BOD≌△CAD,
∴OB=AC,
∵点D的坐标为(-
| 3 |
∴DE=1,OE=
| 3 |
∴在Rt△BDE中,BD=CD=BC=7,由勾股定理,得
BE=4
| 3 |
∴OB=3
| 3 |
∴AC=3
| 3 |
| 3 |
如图,设点C(x,y),在Rt△DHC和Rt△CGB中,由勾股定理,得

|
|
|
∴C(
3
| ||
| 2 |
| 13 |
| 2 |
(3)如图(1)当OA=AC时,△AOC是等腰三角形,
∵OB=AC,
∴OA=OB=2,
∴t=3
| 3 |

如图(2),当B运动到B′时,C点落在OA的垂直平分线上C′时,△AOC是等腰三角形,△DB′C′是等边三角形,连接OC′,
∴四边形DB′OC′是菱形,
∴B′D=B′O=OC′,OE=1,C′E=
| ||
| 3 |
∴OC′=
2
| ||
| 3 |
∴t=
2
| ||
| 3 |
| 3 |
11
| ||
| 3 |
如图(2)当B运动到B″时,B″O=DO,这时AO=AC″,△AOC是等腰三角形,
∴OB″=2,
∴t=OB″+OB=3
| 3 |
如图(2)当B运动到B3时,点C3在AO的中垂线上时,△AOC3是等腰三角形,
∴△B3DO是Rt△,且∠DB3O=60°,∠B3OD=30°,
∴∠B3DO=90°,且OD=2,由勾股定理,得
∴OB3=
4
| ||
| 3 |
∴t=3
| 3 |
4
| ||
| 3 |
13
| ||
| 3 |
∵点B、D、C要沿顺时针方向排列,
∴t值不存在.
当B运动到B5时,DB5=DO=2,C点在第三象限,即C5.
∴∠DB5O=∠B5OD=30°.
∵△B5C5D是等边三角形,
∴∠B5DC5=60°,
∴DC5⊥OB5.
∴由勾股定理可以求出
| 1 |
| 2 |
| 3 |
∴OB5=2
| 3 |
| 3 |
| 3 |
| 3 |
综上所述:∴t1=3
| 3 |
| 11 |
| 3 |
| 3 |
| 3 |
| 3 |
⑤

点评:本题考查了全等三角形的判定与性质,等边三角形的性质,两点间距离公式的运用,等腰三角形的判定与性质及勾股定理的运用.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
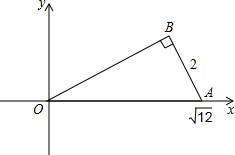 已知在Rt△OAB中,∠B=90°,
已知在Rt△OAB中,∠B=90°,
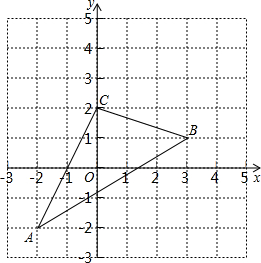 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,