题目内容
 如图,将矩形沿图中虚线剪成四块图形,用这四块图形恰能拼一个正方形.若
如图,将矩形沿图中虚线剪成四块图形,用这四块图形恰能拼一个正方形.若 ,则
,则 的值等于
的值等于
- A.3
- B.

- C.

- D.

C
分析:观察图形可得,两个直角梯形的斜腰重合在一起可以组成一个长为x,宽为y的矩形,两个直角三角形的斜边重合可以组成一个长为x,宽为(x+y)的矩形,两个矩形放在一起恰好可以组成一个边长为x的正方形,然后根据剪拼前后两个图形的面积不变列式求解即可.
解答:由题意得,拼成的正方形的面积与长方形的面积相等,即:x2=(x+y)•y
当x= 时,y=
时,y= ,
,
故选C.
点评:本题考查了图形的剪拼及一元二次方程的应用,根据四块图形的特点,找出可以重合的边,拼接出正方形并得到正方形的边长是解题的关键.
分析:观察图形可得,两个直角梯形的斜腰重合在一起可以组成一个长为x,宽为y的矩形,两个直角三角形的斜边重合可以组成一个长为x,宽为(x+y)的矩形,两个矩形放在一起恰好可以组成一个边长为x的正方形,然后根据剪拼前后两个图形的面积不变列式求解即可.
解答:由题意得,拼成的正方形的面积与长方形的面积相等,即:x2=(x+y)•y
当x=
 时,y=
时,y= ,
,
故选C.
点评:本题考查了图形的剪拼及一元二次方程的应用,根据四块图形的特点,找出可以重合的边,拼接出正方形并得到正方形的边长是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
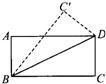 26、如图中的△BDC′是将矩形纸片ABCD沿对角线BD折叠到的.则图中(包括虚,实线)共有
26、如图中的△BDC′是将矩形纸片ABCD沿对角线BD折叠到的.则图中(包括虚,实线)共有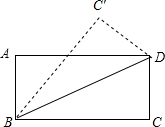 如图中的△BDC′是将矩形纸片ABCD沿对角线BD折叠到的.则图中(包括虚,实线)共有________对全等三角形.
如图中的△BDC′是将矩形纸片ABCD沿对角线BD折叠到的.则图中(包括虚,实线)共有________对全等三角形.
