题目内容
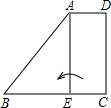如图为梯形纸片ABCD，E点在BC上，且∠AEC=∠C=∠D=90°，AD=3，BC=9，CD=8．若以AE为折线，将C折至BE上，使得CD与AB交于F点，则BF长度为何（ ）| A、4.5 | B、5 | C、5.5 | D、6 |
分析：先根据题意画出示意图，根据轴对称的性质可以得出一些线段的长度，进而根据相似三角形的性质可解得BF的长．
解答：
解：由题意得：EC′=EC=AD=3，
∴BC′=BC-C′E-EC=3，
∴AB=
=10，
又∵△BC′F∽△BEA，
∴
=
，
∴BF=5．
故选B．
解：由题意得：EC′=EC=AD=3，∴BC′=BC-C′E-EC=3，
∴AB=
| AE2+BE2 |
又∵△BC′F∽△BEA，
∴
| BF |
| AB |
| BC′ |
| BE |
∴BF=5．
故选B．
点评：本题考查勾股定理及梯形的知识，难度不大，解答本题的关键是掌握翻折后的对应线段相等，另外还要注意掌握相似三角形的对应边成比例的应用．
练习册系列答案
相关题目
