题目内容
12.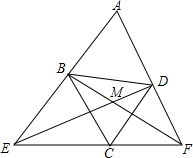 如图,菱形ABCD中∠A=60°,过点C的直线分别交AB、AD的延长线于E、F,BF与DE相交于M.求证:
如图,菱形ABCD中∠A=60°,过点C的直线分别交AB、AD的延长线于E、F,BF与DE相交于M.求证:(1)BD是BE和DF的比例中项;
(2)BD是DM和DE的比例中项.
分析 (1)由四边形ABCD是菱形,得到AB=AD=BC=CD,AB∥CD,AD∥BC,根据平行线的性质得到∠EBC=∠A=∠CDF,∠AEF=∠DCF,于是求得△BCE∽△CDF,得到$\frac{BE}{CD}=\frac{BC}{DF}$,等量代换得到$\frac{BE}{BD}=\frac{BD}{DF}$,于是得到结论;
(2)推出△DBE∽△FBD,根据相似三角形的性质得到∠BED=∠FBD,证得△BDM∽△EBD,得到$\frac{BD}{DE}=\frac{DM}{BD}$,即可得到结论.
解答 解:(1)∵ 四边形ABCD是菱形,
四边形ABCD是菱形,
∴AB=AD=BC=CD,AB∥CD,AD∥BC,
∴∠EBC=∠A=∠CDF,∠AEF=∠DCF,
∴△BCE∽△CDF,
∴$\frac{BE}{CD}=\frac{BC}{DF}$,
∵∠A=60°,
∴△ABD是等边三角形,
∴BD=BC=CD,
∴$\frac{BE}{BD}=\frac{BD}{DF}$,
∴BD2=BE•DF,
即BD是BE和DF的比例中项;
(2)∵$\frac{BE}{BD}=\frac{BD}{DF}$,
∵∠EBD=∠BDF=120°,
∴△DBE∽△FBD,
∴∠BED=∠FBD,
∵∠BDM=∠BDE,
∴△BDM∽△EBD,
∴$\frac{BD}{DE}=\frac{DM}{BD}$,
∴BD2=DE•DM,
即BD是DM和DE的比例中项.
点评 本题考查了相似三角形的判定和性质,菱形的性质,等边三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
20.下列说法中正确的选项是( )
| A. | 温度由-3℃上升3℃后达到-6℃ | |
| B. | 零减去一个数得这个数的相反数 | |
| C. | $\frac{π}{3}$既是分数,又是有理数 | |
| D. | 20.12既不是整数,也不是分数,所以它不是有理数 |
2.某车间的生产任务是平均每天生产某种零件200个;由于各种原因,实际每天生产量与计划量相比有出入,下表是某一周的生产情况纪录(超产为正,不足为负).
(1)根据记录情况,前两天共生产零件403个;
(2)产量最多的一天比产量最少的一天多生产26个;
(3)为调动工人生产积极性,该车间实行计件工资制,即每生产l个零件记60元,超额完成任务的每个另外奖15元,少生产一个扣15元,则该车间工人这一周的工资总额是多少元?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -8 |
(2)产量最多的一天比产量最少的一天多生产26个;
(3)为调动工人生产积极性,该车间实行计件工资制,即每生产l个零件记60元,超额完成任务的每个另外奖15元,少生产一个扣15元,则该车间工人这一周的工资总额是多少元?