Question

【题目】如图，己知抛物线经过点A(l, 0)，B(一3,0)，C(0,3)三点.

（1）求抛物线的解析式;

（2）在x轴下方的抛物线上，是否存在点M，使得？若存在求出M点的坐标；若不存在，请说明理由；

（3）点P是位于直线BC上方的抛物线上的一个动点，是否存在点P，使的面积最大?若存在，求出P的坐标及的最大值:若不存在，说明理由.

Answer 1

【答案】(1)

（2）M点的坐标为：（-4，-5），（2，-5）.

（3）当时， 最大，最大值为。

【解析】试题分析：（1）由抛物线经过三点，可设抛物线的解析式为，将A、B、C三点带入方程即可求得a、b、c的值；

（2）设存在点M(a，b)，由题意可知， 以AB=4为底，则高为OC=3，因此=10 ，又在中，以AB=4为底，则高为，所以=，因为M点在x轴的下方，故b<0,因此b=-5，又因为M在抛物线上，所以满足抛物线方程。代入得： ，解得， ，即可得到M点的坐标；

（3）连接PC、PB，过P作PR⊥x轴，交BC于点Q，可知当PQ有最大值时， 有最大值，由待定系数法求得直线BC的解析式，设出点P的坐标，进而得出Q点坐标，表示出 PQ的长度，求出最大值，即可解决问题.

试题分析：（1）设抛物线方程为，

将A(l，0)，B(-3，0)，C(0，3)带入方程得： ，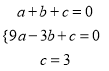

解得，所以抛物线的解析式为： ；

（2）设存在点M(a，b)，由题意可知， =×4×3=6，

∴=， =5，

因为M点在x轴的下方，故b<0,因此b=-5，

又因为M在抛物线上，所以满足抛物线方程，

代入得： ，解得， ，

所以M点的坐标为：（-4，-5），（2，-5）.

（3）如图：

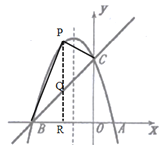
连接PC、PB，过P作PR⊥x轴，交BC于点Q，

设直线BC的解析式为：y=kx+m，把B（-3，0），C（0，3）代入，

则，

解得： ，

则直线BC的解析式是y=x+3.

设点P的坐标为（x， ），则Q坐标为（x），

PQ==-(x+)2+，

当x=-时，PQ有最大值，此时有最大值为： ××3=.