题目内容
如图，在⊙O中，直径BC为10，点A是⊙O上的一个点，∠ABC的平分线交⊙O于点E，交AC于点F．过点E作⊙O的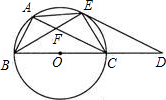
切线，交BC的延长线于虑D，连接CE．（1）求证：∠ACE=∠DEC′；
（2）若AB=AE，求AF的长；
（3）如果点A由点B出发，在⊙O的圆周上运动，当点A在什么位置时，AE与BD互相平行？
分析：（1）根据角平分线的性质可知∠ABE=∠EBC，
=
，由圆周角定理可得∠ABE=∠ACE，由弦切角定理可知∠DEC=∠EBC，故∠ACE=∠DEC；
（2）由（1）可知
=
，因为AB=AE，所以
=
=
，故A、E三等分
，故三段弧所对的圆周角等于30°，再根据直角三角形及相似三角形的性质即可解答；
（3）由（2）可知，当
=
=
，即A、E三等分
时，AE与BD互相平行．
 |
| AE |
|
| CE |
（2）由（1）可知
|
| AE |
|
| CE |
|
| AE |
|
| CE |
|
| AB |
|
| AC |
（3）由（2）可知，当
|
| AE |
|
| CE |
|
| AB |
|
| AC |
解答：（1）证明：∵AE是∠ABC的平分线，
∴∠ABE=∠EBC，
=
；
又∵∠ABE=∠ACE，∠DEC=∠EBC，
∴∠ACE=∠DEC．
（2）解：∵
=
，AB=AE，
∴
=
=
，故A、E三等分
，
∴∠EBC=∠ACB=∠CAE=∠AEB=30°，AE∥BD；
在Rt△ABC中，∠ACB=30°，故AB=
BC=
×10=5，故AB=AE=CE=5，
AC=BE=
=
=5
，
△AEF∽△CBF，设AF=x，则
=
，即
=
，
解得x=
，即AF=
；
（3）解：由（2）可知，当
=
=
，即A、E三等分
时，AE与BD互相平行．
∴∠ABE=∠EBC，
|
| AE |
|
| CE |
又∵∠ABE=∠ACE，∠DEC=∠EBC，
∴∠ACE=∠DEC．
（2）解：∵
|
| AE |
|
| CE |
∴
|
| AE |
|
| CE |
|
| AB |
|
| AC |
∴∠EBC=∠ACB=∠CAE=∠AEB=30°，AE∥BD；
在Rt△ABC中，∠ACB=30°，故AB=
| 1 |
| 2 |
| 1 |
| 2 |
AC=BE=
| BC2-AB2 |
| 102-52 |
| 3 |
△AEF∽△CBF，设AF=x，则
| AF |
| CF |
| AE |
| BC |
| x | ||
5
|
| 1 |
| 2 |
解得x=
5
| ||
| 3 |
5
| ||
| 3 |
（3）解：由（2）可知，当
|
| AE |
|
| CE |
|
| AB |
|
| AC |
点评：此题比较复杂，涉及到圆周角的性质定理及直角三角形的性质，是中学阶段的重点内容．
练习册系列答案
阅读快车系列答案
相关题目
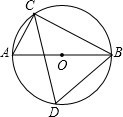如图，在⊙O中，直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，则BC=
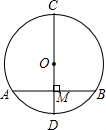如图，在⊙O中，直径CD的长度为10cm，AB是弦，且AB⊥CD于M，OM=3cm，求弦AB的长．
C与直线AB相交于点G．
（2013•百色）如图，在⊙O中，直径CD垂直于弦AB，若∠C=25°，则∠ABO的度数是（ ）
（2012•朝阳区二模）如图，在⊙O中，直径AB⊥弦CD于点H，E是⊙O上的点，若∠BEC=25°，则∠BAD的度数为（ ）